0.08/100 for my maths degree at Warwick University
Cryptography Project Reflections
I am writing this to share with you my reflections on my maths group project at the University of Warwick. This individual submission counts for 0.08/100 of my entire maths degree.
Read on to find out more!
1. Contribution to the Project
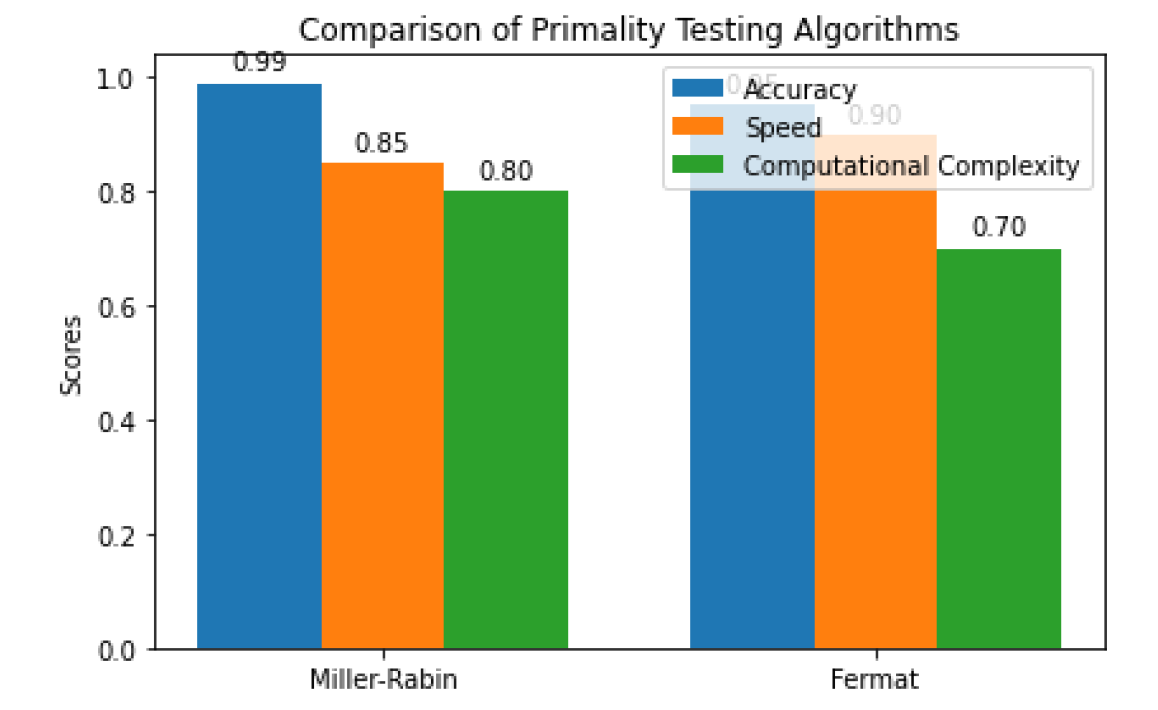
My primary contribution to the project was focused on primality testing and exploring various algorithms used in this context. I conducted a literature review on primality testing techniques, such as the AKS primality test, the Miller-Rabin primality test, and the Fermat primality test. Based on the findings, I developed a comparative analysis of these algorithms, evaluating their efficiency, accuracy, and computational complexity. Additionally, I implemented the chosen primality test algorithm in our team's cryptographic solution, ensuring the generation of suitable prime numbers for cryptographic key pairs.
We can see a difference in the time it takes to test for primality.
2. Improvements in Group Dynamics
While our group collaboration was generally effective, there were areas where we could have improved our teamwork. One such place was in communication and task delegation. By implementing a more formalized system for assigning tasks and setting deadlines, we could have better managed our collective workload and ensured all team members understood their responsibilities. Furthermore, holding regular meetings to discuss progress, challenges, and potential solutions would have facilitated a more efficient and collaborative working environment.
3. Project Highlights and Interests
The aspect of the project that I found most intriguing was the exploration of various primality testing algorithms and their impact on cryptographic systems. Examining the different approaches to primality testing and understanding the trade-offs between accuracy, speed, and computational complexity provided valuable insights into the design of secure cryptographic systems. It was fascinating to learn how the choice of primality test could influence the overall security, efficiency, and practicality of a cryptographic solution.
The charts were generated using Python.
4. Areas for Further Exploration
In light of the work done on this project, I am eager to explore further the implications of different primality testing algorithms and their potential applications in cryptography. Specifically, I would like to investigate how these algorithms can be optimized for specific use cases or hardware constraints, ultimately improving the security and efficiency of cryptographic systems. Additionally, I am interested in examining other areas of number theory and their relevance to cryptography, such as factoring algorithms, discrete logarithm problems, and elliptic curve cryptography. By deepening my understanding of these topics, I hope to contribute to the ongoing development of innovative and secure cryptographic solutions.
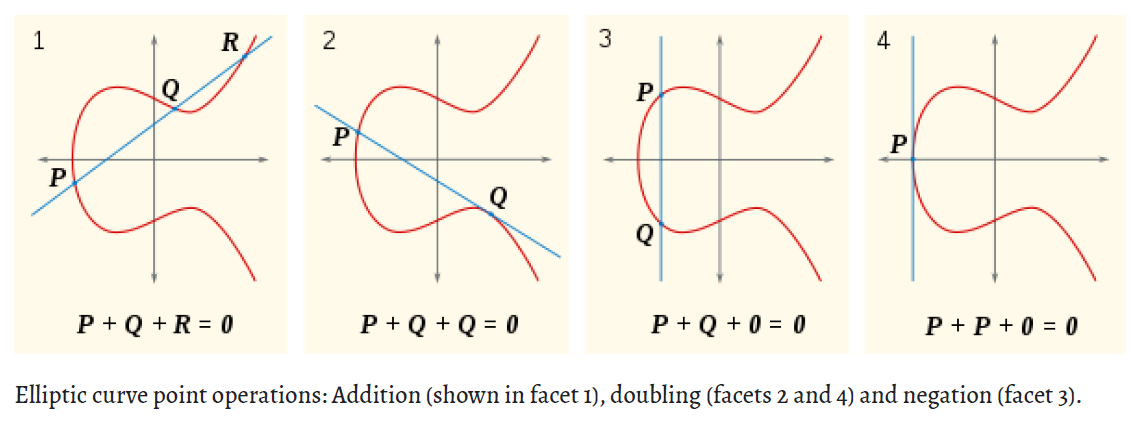
In particular, I spent some time looking more into elliptic curve cryptography after today's presentation.
Point Addition
Point addition in ECC involves adding two points on the curve, say P and Q, to obtain a third point R. To visualize this process, imagine drawing a straight line that passes through points P and Q. This line will intersect the curve at a third point, say -R (the negative of R). Now, if we reflect -R over the x-axis, we will get the point R, which is the result of the addition (P + Q = R).
Point Doubling
Point doubling is the operation of adding a point P to itself to obtain a new point R (P + P = R). To perform point doubling, we draw a tangent line to the curve at point P. Th is a tangent line that will intersect he curve at a point -R. By reflecting -R over the x-axis, we get the point R, which is the result of the doubling operation.
This is a free newsletter, but if you would like to be one of my early supporters, consider becoming a paid member so that I can continue to bring out quality mathematical treats. 🍩
Happy reading,
Barry 🍩