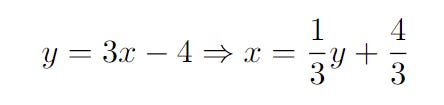#10 What Is g(x)?
Composition of Functions
Today’s Question
Today’s question focuses on understanding the nature of functions and their compositions.
Think of a function as a rule that maps an input to a particular output. Now, what happens when the input of a function is another function?
Give this problem a try before jumping in for the solution!
Solution
f(x) = ax + b is a linear function and we are given f(f(f(x))) = 27x - 52.
Let’s first look at what f(f(x)) means in terms of a, b and x.
Now, our new input becomes ax + b.
We now once again apply the same process for f(f(f(x))).
This results in the following.
Because the above expression and 27x -52 have the same value for all real numbers x, we can compare the coefficients.
For the x term, we have
For the constant term, we have
Substitute a = 3 into the equation and we get
Now that we have the values of a and b, we know what f(x) is.
This leads us to the final step of our problem. If g(f(x)) = x, this means
How would you find g(x)? Pause and think for a second.
In fact, we can use a variable y such that y = 3x - 4.
By rearranging the equation in terms of y, we can represent the function g in terms of y.
In this case, y is simply an arbitrary variable, so our answer is the following.
So the answer is B. Well done!
Thank you for reading. This is a semi-free newsletter, but if you would like to read more of my work, consider becoming a paid member for less than the price of 2 coffees a month (£5/$4). This is a great way to fuel my writing and you get to have access to all paid posts. I will thank you a million times.
☕ Make a one-time coffee donation
Happy reading,
Barry 🍩