#12 What was the original depth of the water in the larger vase?
2 Cylindrical Vases
Today’s Question
This problem is about volume and the key to this question is to know that the volume of water remains the same throughout.
Give this problem a try before jumping in for the solution!
Solution
Recall the formula for the volume of a cylinder.
r is the radius and h is the height.
To help us solve this problem, we can express the radius in terms of the diameter.
We then substitute this expression into the formula for the volume.
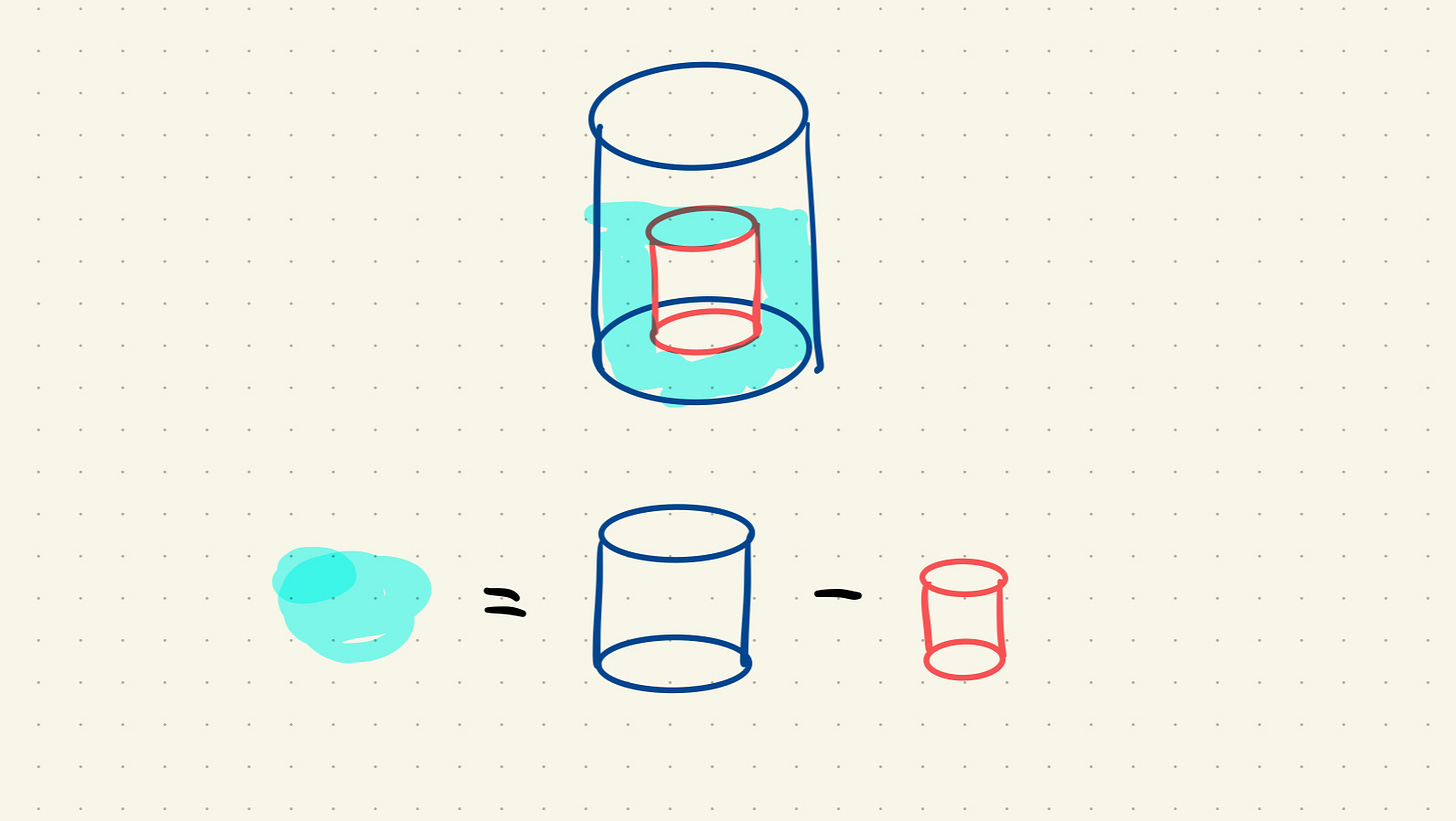
When the smaller vase is pushed right down and the water finishes flowing over the rim, the water in the larger vase comes to the top of the smaller cylinder and so has the same depth as the height of the smaller cylinder, which is 16 cm.
As you can see, I have painted the surface of the water remaining in the outer vase yellow. It just stays at exactly the same height as the inner cylinder.
This means that the volume of water in the larger vase is that of a cylinder with a diameter of 20 cm and height of 16 cm, less the volume of the empty half of the smaller vase
Now let’s say the original depth of water before the smaller vase is pushed down is x. Then the volume of water in terms of x is
With this, we can equate the two equations and find the original depth of the water.
And so the original depth was 14 cm. Well done.
Thank you for reading. This is a semi-free newsletter, but if you would like to read more of my work, consider becoming a paid member for less than the price of 2 coffees a month (£5/$4). This is a great way to fuel my writing and you get to have access to all paid posts. I will thank you a million times.
☕ Make a one-time coffee donation
Happy reading,
Barry 🍩