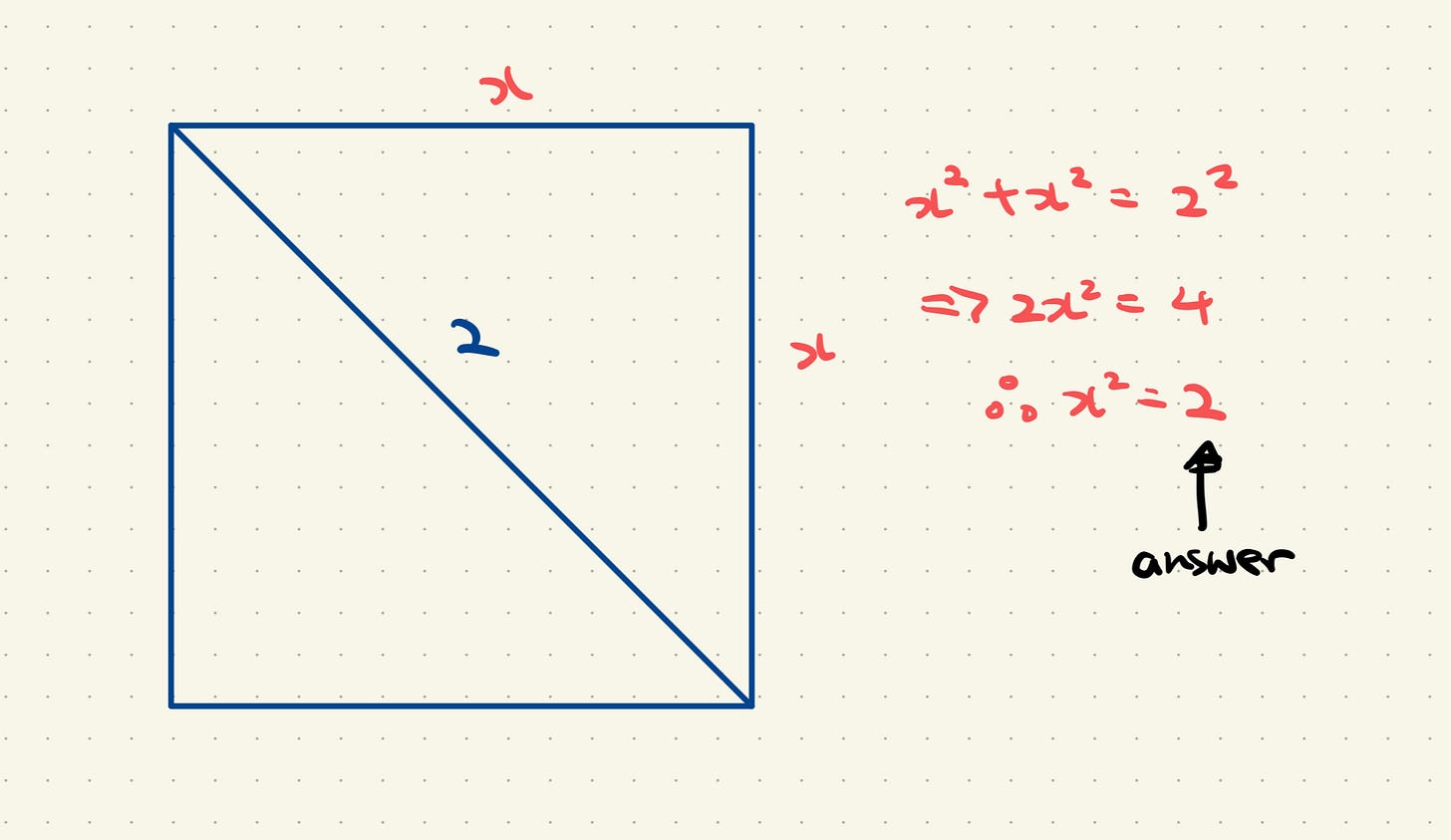#8 What Is The Shaded Area Of A Baseball?
A Geometry Question
Today’s Question
Let’s take a look at a geometry puzzle today.
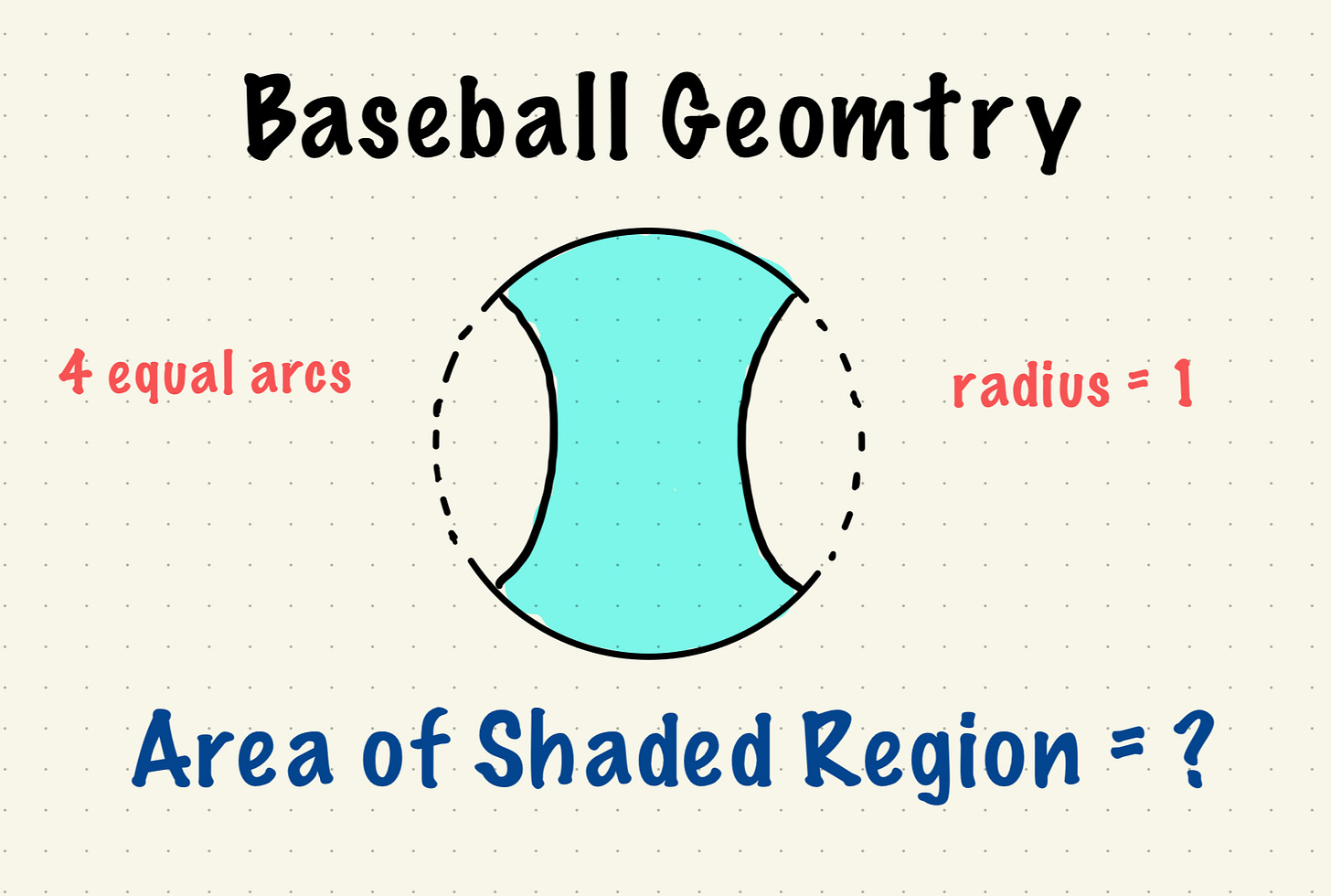
The circumference of a circle with radius 1 is divided into four equal arcs. Two of the arcs are ‘turned over’ as shown. What is the area of the shaded region?
Give this problem a try before jumping in for the solution!
Solution
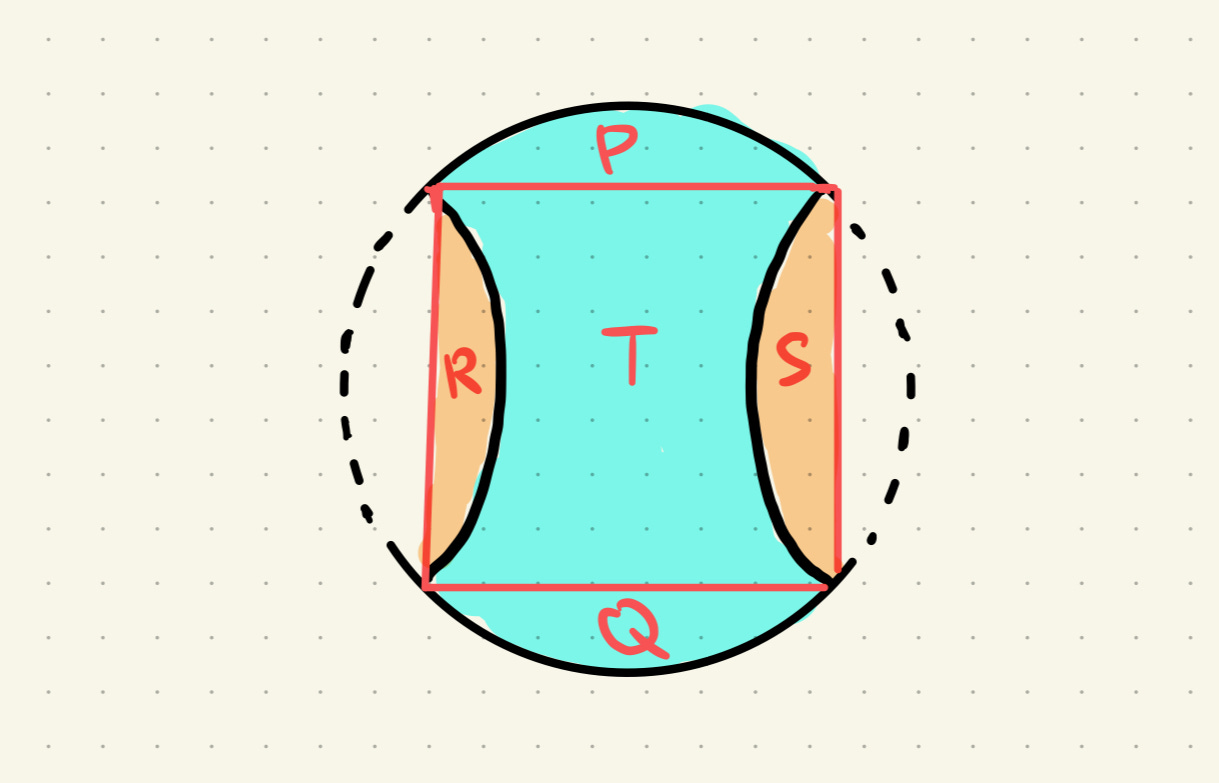
The question tells us that the four arcs are equal, meaning their endpoints must form a square.
By symmetry, the four segments, P, Q, R, S are congruent. Now the shaded area in blue is what we want to find.
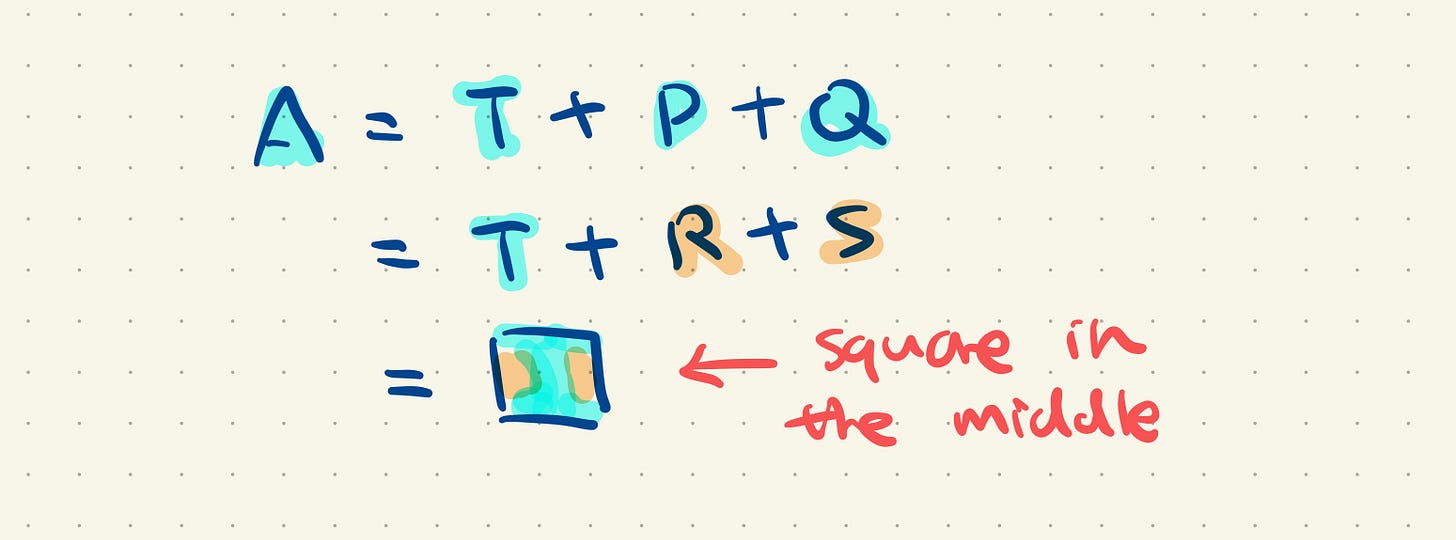
It turns out that the area of this region is equal to that of the square which is made up of T and the two segments R and S.
So we have now simplified the problem into finding the area of a square, and this is what makes mathematics so fascinating!
The radius of the circle is 1, which means the diagonal of the square is 2!
Now, by applying Pythagoras theorem, we find the area of the square as 2, which is equal to the area of the shaded region.
Well done!
P.S. I can finally write up problems more consistently, please consider becoming a paid member to fuel my great maths puzzles :) Thank you very much. I have finalised the price of 5GBP a month or 50GBP a year for a discount.
Thank you for reading. This is a semi-free newsletter, but if you would like to read more of my work, consider becoming a paid member. This is a great way to support me as a university student and you get to have access to my premium newsletters and maths puzzles!
☕ Make a one-time coffee donation
Happy reading,
Barry 🍩