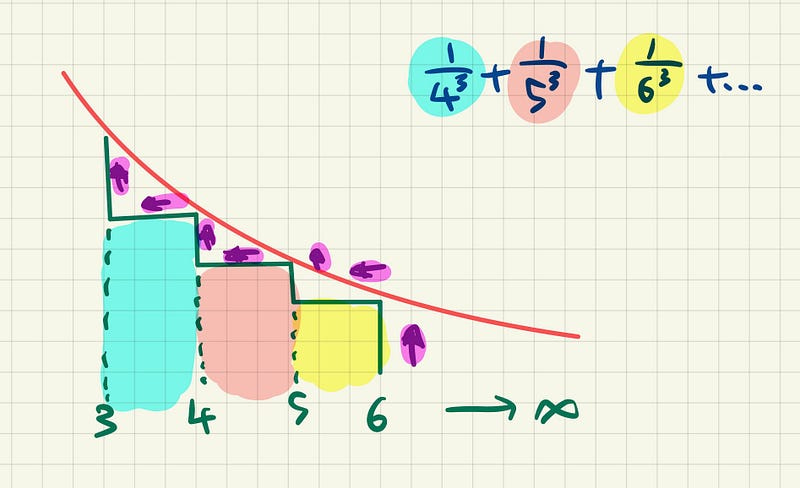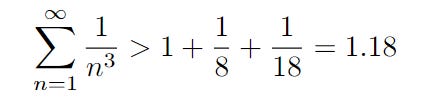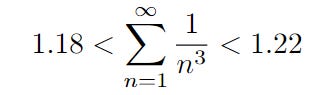A 2008 International Baccalaureate Higher Level Maths Paper
Is University Maths Getting Easier?
Today’s Challenge
I study mathematics at the University of Warwick. One of my courses is Real Analysis, where we have looked at concepts like sequences, series, summation, convergence, continuity and many more.
The above problem is taken from a 2008 International Baccalaureate Higher Level Maths Exam. It is an optional module known as Series and Differential Equations, a test taken by high school maths students.
It seems like more advanced maths concepts previously taught at the high school level are now being pushed back. Anyway, let’s hope everyone can learn something from today’s problem!
Part(A): Using The Diagram
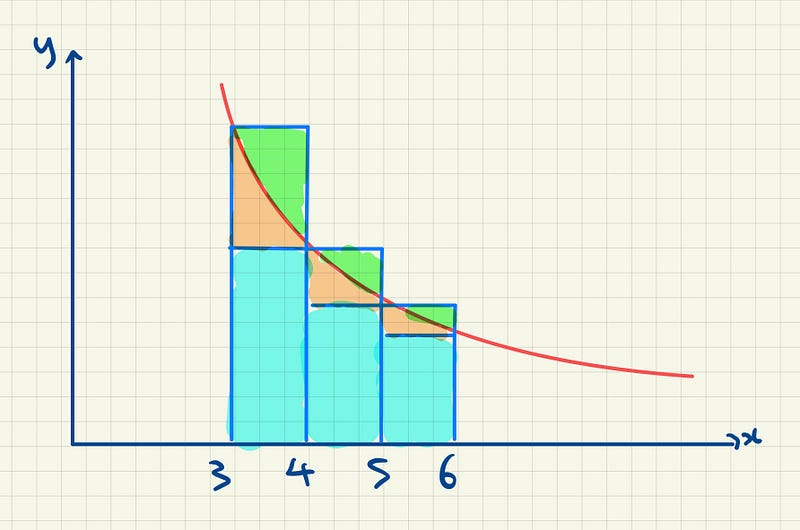
We are given the curve y = 1/x³ and have to show that the integral is bounded between the two series.
Let’s annotate the diagram and really understand how it all works out
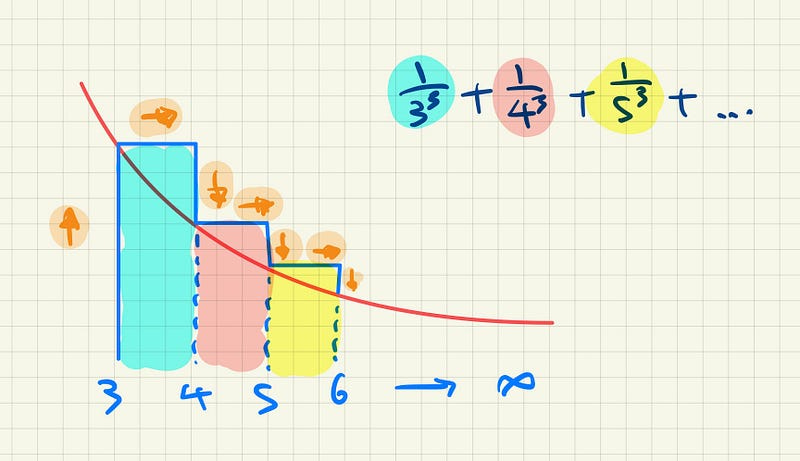
For simplicity’s sake, we will consider intervals 3 to 6. Notice that the integral of the function from 3 to 6 is the sum of the blue rectangles and the orange bits sandwiched between the green parts and blue parts.
The upper bound of the series includes the extended part of the rectangle, denoted in green. If we start at 3, we can imagine the blue line shooting up to the top of the curve and moving back down at a distance of one integer apart, repeating the process ad infinitum
Equally, we can make sense of the lower bound by starting at 6, going in the opposite direction this time. As soon as the green line touches the curve, it shoots to the left, then goes up and repeats the same process, ad infinitum
Based on these two graphs, we can safely conclude that
Part(B):
Interestingly, this part is an extension or an application of the result proved in the first part.
We first start by evaluating the improper integral
We will now consider the series by writing out the first few terms
Combined with the value of the integral as well as the result in part (a), we can say that
That’s our upper bound!
In a similar fashion, we can group the terms as follows
which gives us the following lower bound
Therefore
Well done!
An Epilogue: Let’s Compare My Uni Assignments To This Question
As we can see maths at the university level is still more rigorous than the question we just did. What do you think? Comment down below!
This is a free newsletter, but if you would like to be one of my early supporters, consider becoming a paid member so that I can continue to bring out quality mathematical treats.
Happy reading,
Barry 🍩