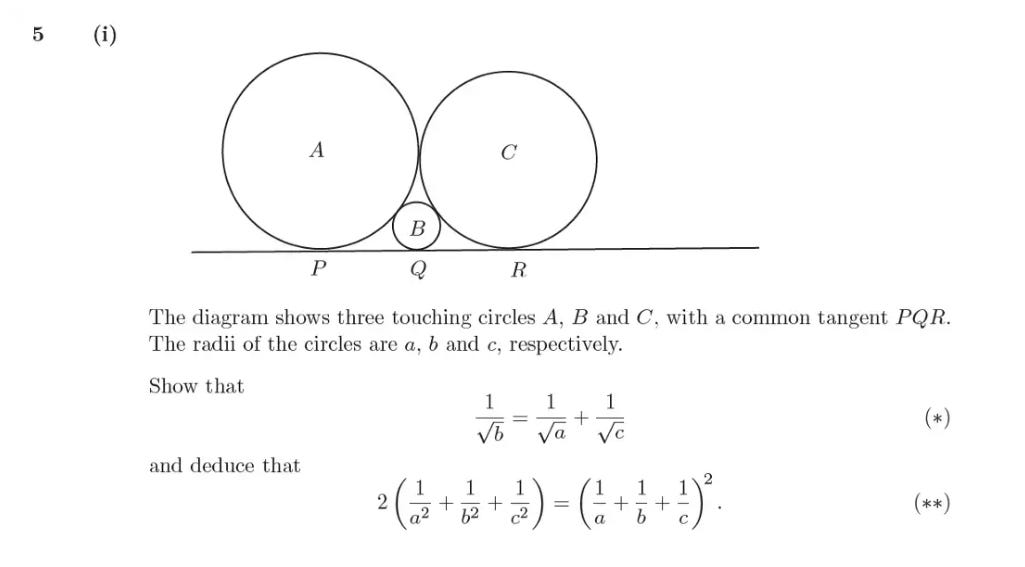
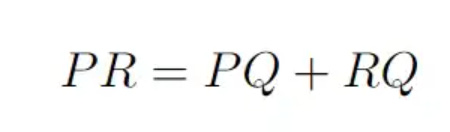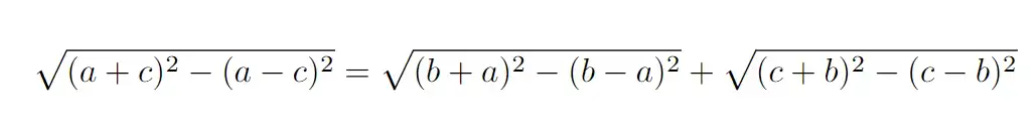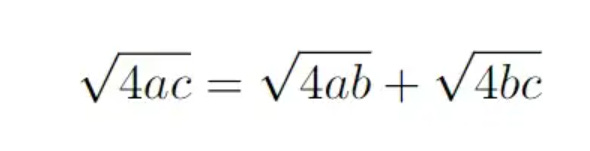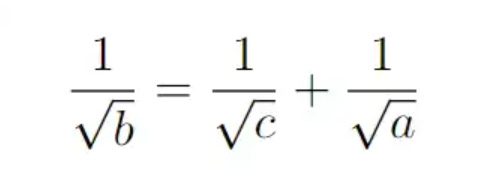A Cambridge University Admission Question
Proving an Elegant Result in Circle Geometry
Today’s Challenge
I was looking at some STEP past papers and came across this interesting question. This is one of those classic problems in geometry that I think you should know about!
If you want to hone in on your geometry skills and get better at maths olympiad, definitely read on!
I will only focus on part 1 of the problem, the second equality is left to you the reader to figure out.
Give this problem a try before jumping in for the solution!
Solution
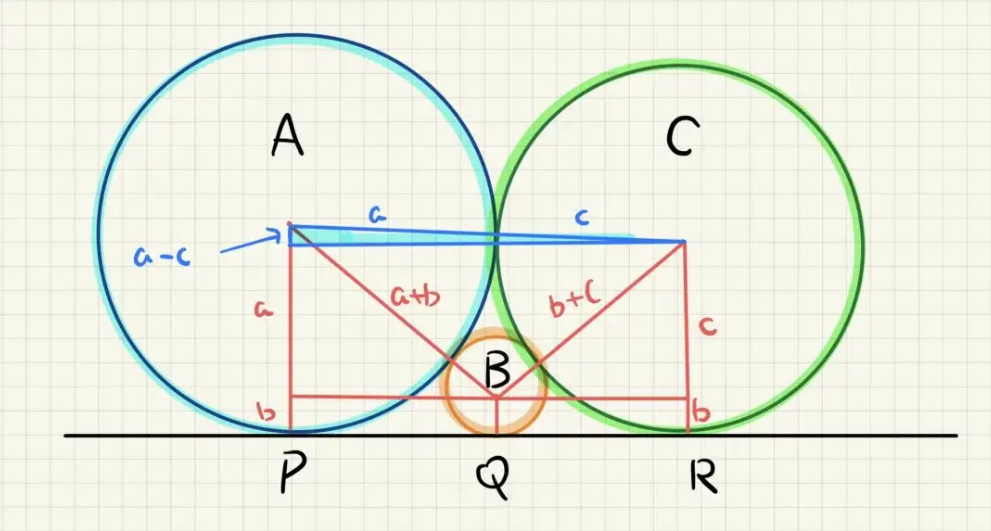
The conventional approach is to connect all the circles’ centres to the points of tangential contact. We can then form a couple of right-angled triangles as shown above.
Pause the article to get an understanding of what’s really going on.
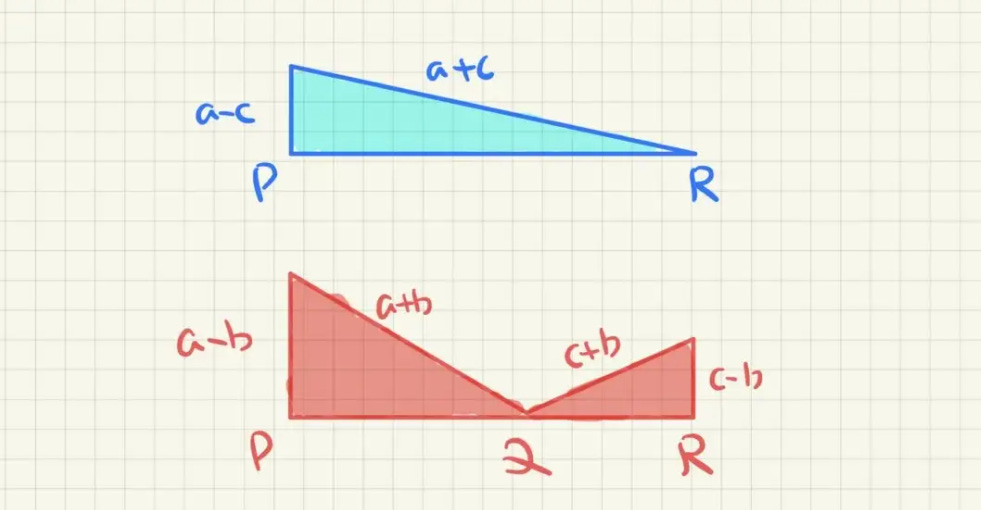
We now consider 3 triangles. Two in red and one in blue.
Notice that the base of the blue triangle is the sum of the bases of the two red triangles.
Mathematically, that is
The trick is that we can apply Pythagoras’ Thereom for each length.
The squared terms in these expressions cancel out, we are only left with the ‘middle’ bit, which are 2ac + 2ac, 2ab + 2ab and 2bc + 2bc.
Therefore, we have
Notice each term is missing one of the letters, the idea is that we can divide an expression with all the letters.
In fact, we divide by sqrt(4abc), giving us the following identity.
And we are done. Good job.
How would you approach the second part? Leave your comments below!
This is a free newsletter, but if you would like to be one of my early supporters, consider becoming a paid member so that I can continue to bring out quality mathematical treats. 🍩
Happy reading,
Barry 🍩