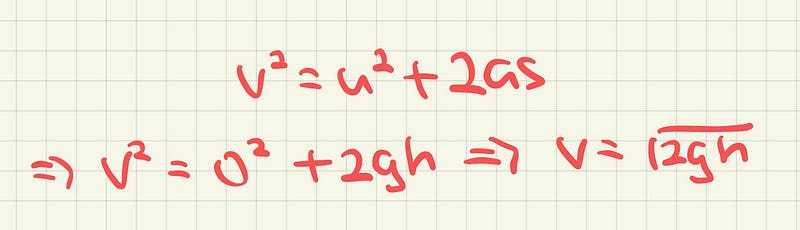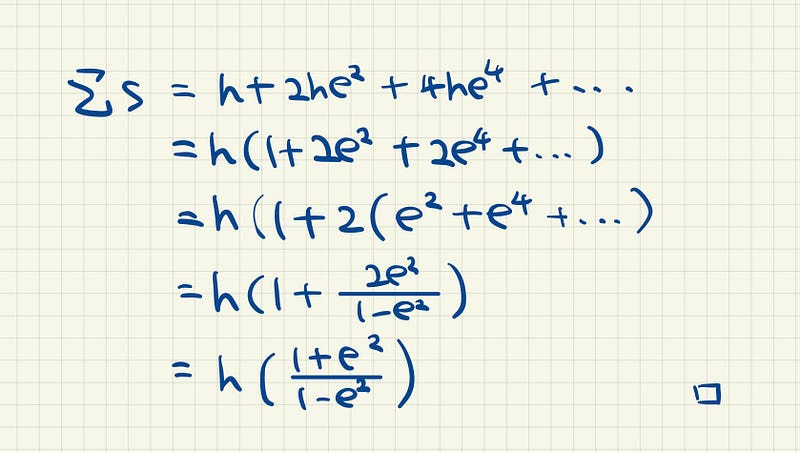A Must-See Classic Problem In Mechanics & Collisions
From My A-level Studies
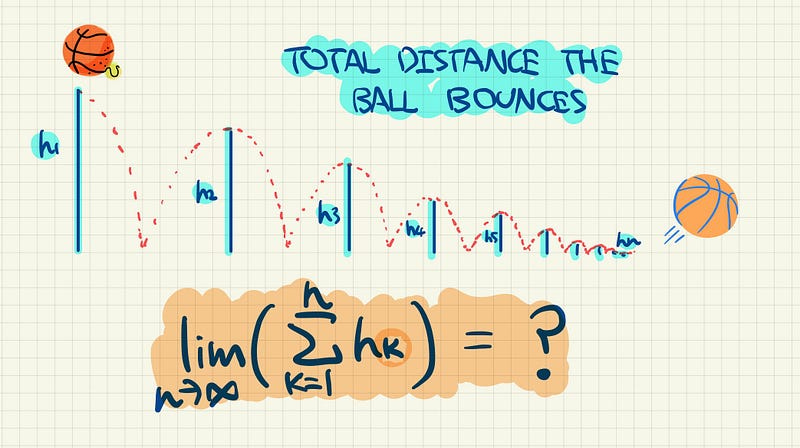
Today’s Challenge
I credit this problem to my former mechanics teacher, who went through this classic problem with us in our lesson on collisions and the coefficient of restitution.
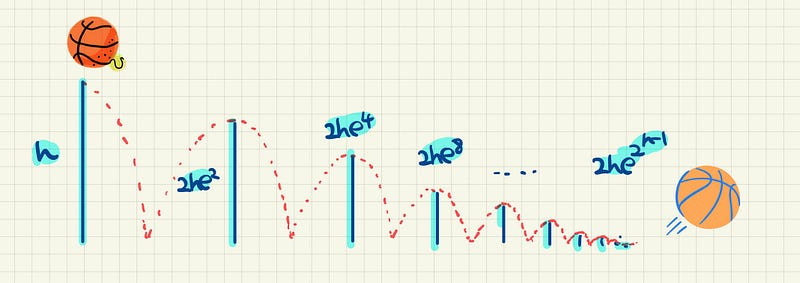
A ball is dropped from height h to the ground, and the coefficient of restitution of the ground and the ball is e. As the ball keeps bouncing, it eventually comes to a stop. What is the total distance the ball has travelled as it bounces?
Give this problem a try before jumping in for the solution!
Solution
This is a very good exercise that tests our understanding of mechanics and mathematics in general. To solve this problem, we can first consider the first few sections of distances covered by the ball as it drops.
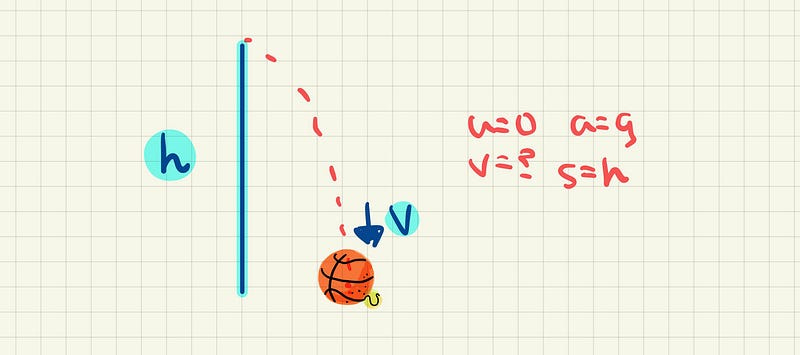
As the ball first drops to the ground, it is given that the distance is h. We now want to look at the second section of distance. Specifically, that is the distance as the ball goes back up and drops back down again for the second time. Notice the two are equal in length so we really only need to consider the first part as the ball goes back up.
We want to first find out the velocity of the ball as it hits the ground, the idea is that we can multiply this by e, the coefficient of restitution to get the initial velocity as it goes back up.
We are given the acceleration, the initial velocity as well as the distance. We can therefore use the following SUVAT formula.
Now that we have the velocity as it strikes the ground, we multiply it by e to get the initial velocity as it goes back up.
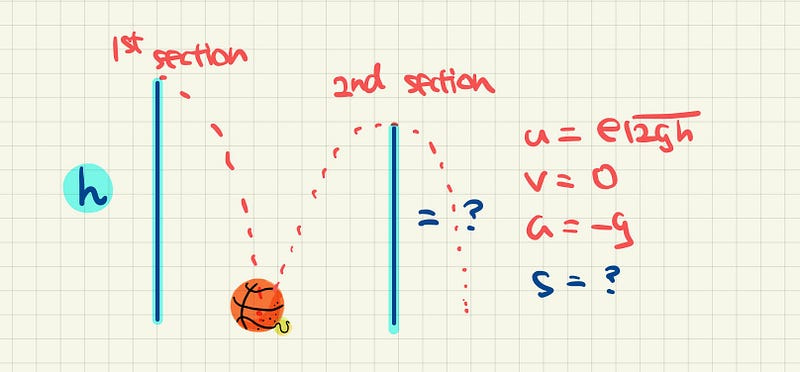
As it goes back up, we expect the height to be slightly less than h, due to factors like friction and energy lost to the surroundings.
We now want to find the height of this bounce. We are given the initial velocity, the final velocity as well as the acceleration. We can apply the same SUVAT equation and get the following
Since it goes up and strikes back down again, the total distance travelled in this section is double this value.
Let’s pause and think for a second. This means as it falls back down again for the second time, the distance is 2he². What does that tell us about the third section? The fourth and the nth?
Do you notice a pattern? In fact, each section is the previous one multiplied by e². (You can prove this via induction, but that’s not the scope of this article.)
So the total distance is in fact an infinite geometric series!
This formula tells us that as e gets closer and closer to 1, the distance travel would get bigger and bigger. In fact, if the coefficient of restitution was 1, the distance would be infinite since it would just keep bouncing at a height of h!
That’s it and we are done. Good job!
This is a free newsletter, but if you would like to be one of my early supporters, consider becoming a paid member so that I can continue to bring out quality mathematical treats.
Happy reading,
Barry 🍩