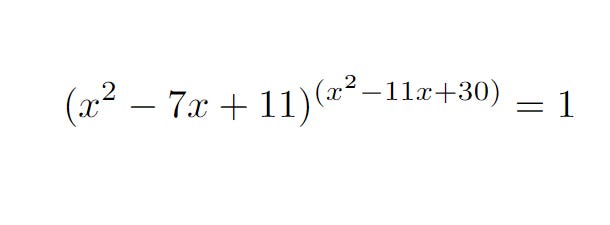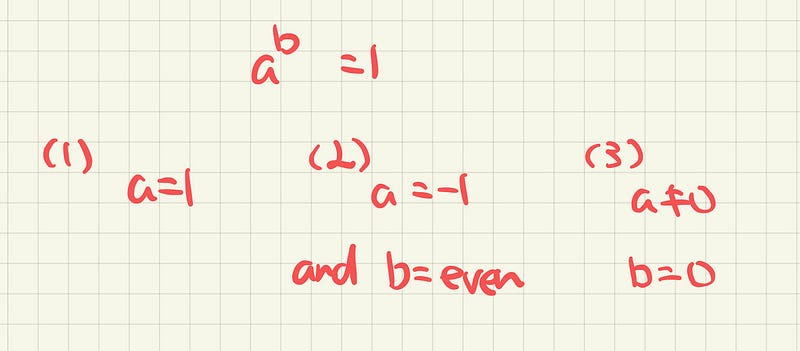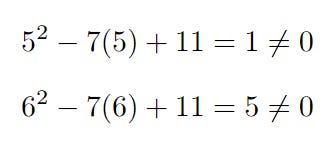A Must Solve Question
Can You Do It?
Today’s Challenge
Let’s look at this classical problem in algebra!
Solution
To solve this problem, think of all the scenarios in which we get 1 on the right-hand side. With some careful thought, we can deduce that
As we can see, there are 3 cases in which we achieve 1.
Let’s look at case 1. We need to have a = 1, meaning
Upon factorization, we get
Therefore 2 and 5 are 2 of the solutions
Let’s move on to case 2. We need to have a = -1 and check that b is even
Upon factorization, we get
So x = 4 and x = 3 are 2 potential solutions
Let’s check that they fulfil b = even
As we can see, b is an even number for x = 4 and x = 3, therefore x = 4 and x = 3 are indeed solutions
Finally, we look at case 3 where we require b = 0 and a ≠ 0
Upon factorization, we get
There x = 5 and x = 6 are 2 potential solutions
Let’s now check that a ≠ 0
Therefore, we have our final set of solutions!
Well done!
This is a free newsletter, but if you would like to be one of my early supporters, consider becoming a paid member so that I can continue to bring out quality mathematical treats.
Happy reading,
Barry 🍩