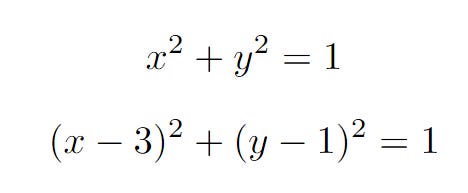A Very Very Tricky Oxford University Maths Question
Oxford MAT 2022 🦅
Today’s Challenge
Let’s look at an Oxford University admission question from Oxford MAT 2022.
Give this problem a try before jumping in for the solution!
Solution
This is the last question in the first 10 MCQs, which is usually the trickiest or hardest. In particular, one might be tempted to use the idea of discriminant and find individual pairs of ms and cs. However, notice the question is specifically asking for the possibilities for the line y = mx +c which satisfies the given conditions.
If we substitute y = mx + c into the two equations, we get
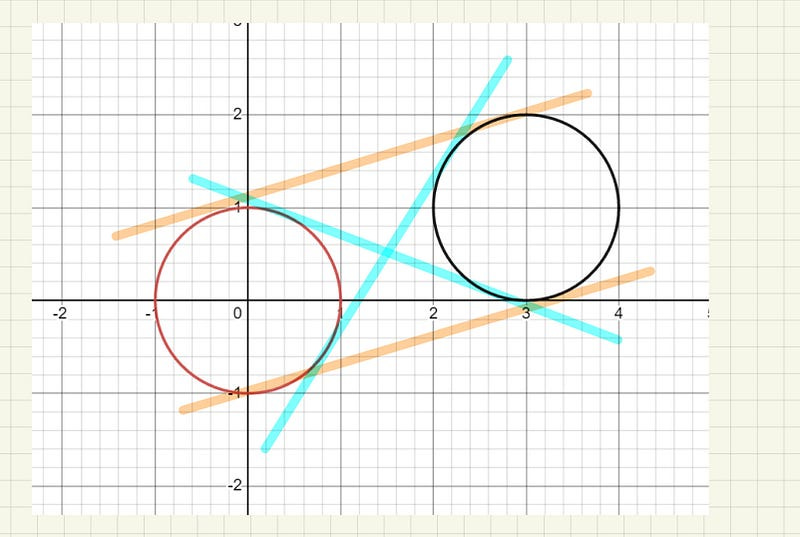
These are two circles with radius one, one centred at the origin and the other centred at (3,1). If we plot them on a graph, we see that
These are two non-overlapping circles. Now, think carefully about what the question really is asking.
In fact, this is equivalent to asking, given an arbitrary straight-line equation, how many ways can we manipulate m and c in y = mx + c such that the line touches the two circles?
We want the line to touch two circles because it states that m and c are values such that both equations have a repeated root.
If the line crosses the circle, that’s not a repeated root. That’s when the discriminant is greater than zero.
So, how many lines can we fit between the two circles such that the lines just touch both of them?
There are indeed four such lines!
Here’s a challenge for all of us. Can you find the equations of those four straight lines? (I haven’t done that, but it’d be great if some of you could try it out!)
Therefore, there are four sets of values of ms and cs that satisfy the equations.
The answer is (e).
Well done!
This is a free newsletter, but if you would like to be one of my early supporters, consider becoming a paid member so that I can continue to bring out quality mathematical treats.
Happy reading,
Barry 🍩