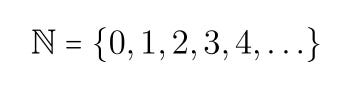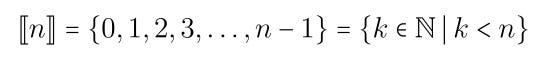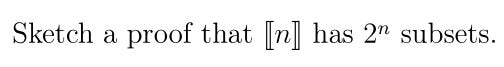Day 1: Sets and Subsets
Foundations of Pure Mathematics

Set Theory
Set theory is a branch of mathematical logic that studies sets, which informally are collections of objects. Although any type of object can be collected into a set, set theory is applied most often to objects that are relevant to mathematics. The language of set theory can be used to define nearly all mathematical objects.
The modern study of set theory was initiated by Georg Cantor and Richard Dedekind in the 19th century. It has been a part of the foundational language of mathematics ever since. Set theory has also been used as a foundation for the development of other branches of mathematics, such as category theory and topology.
What is a Set?
In set theory, a set is usually indicated by a capital letter. The objects contained in a set are called their elements or members. For example, the set of all even numbers can be written as {2, 4, 6, 8, ...}. Sets can be finite, infinite, or empty.
We take N to be the set of natural numbers as shown above.
Question 1
Suppose that X and Y are empty sets. Prove that X = Y.
Solution
Suppose that X and Y are empty sets. Then every element of X belongs to Y. Similarly, every element of Y belongs to X. Thus, by the axiom of extension X = Y.
Question 2
Suppose that X is a set. (1) Prove that the empty set is a subset of X. (2) Prove that X is a subset of X.
Solution
(1) To prove that the empty set is a subset of X, we must check that, for every x in the empty set, that x also lies in X. Since there are no elements of the empty set, no checks can be made. Thus all checks are successful. Ergo, the empty set is in set X, as desired.
(2) To prove that X is a subset of itself, we must check that for every x in X, that x lies in X. This holds evidently, therefore we are done.
Question 3
For Question 3, we need the following definition. For any natural number n, we define
It denotes the subset of the natural numbers which are less than n. For example [0] is just another name for the empty set, whereas [3] = {0, 1, 2}.
Solution
Suppose that Y is a subset of [n]
For each k < n, either k is in Y or it is not. All of these possibilities are independent: that is, for any collection of n two-fold choices there is such a subset Y. Thus there are
subsets of [n].
Thank you for reading. Stay tuned for Day 2’s email on power sets, specification and functions.
This is a free newsletter, but if you would like to be one of my early supporters, consider becoming a paid member so that I can continue to bring out quality mathematical treats. 🍩
Happy reading,
Barry 🍩