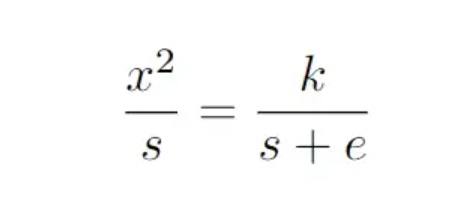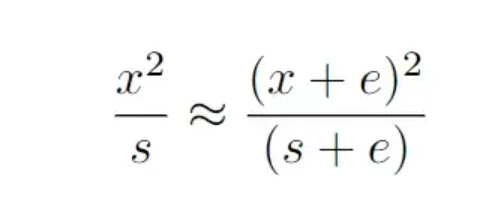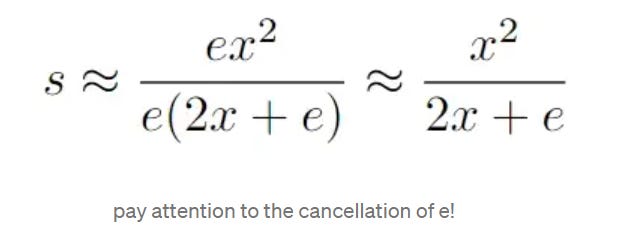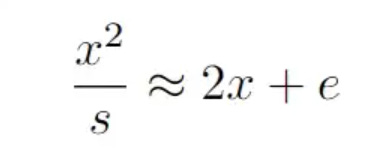Fermat under Attack: Tangent Method
Beginnings of Calculus
Ancient Calculus by Fermat
Let’s travel back in time to witness the humble beginnings of calculus.
This time, we are looking at the work of Pierre de Fermat, his first-ever method to systematically tackle the problem of tangents.
Without further ado, let’s dive in!
Pierre de Fermat
Pierre de Fermat was a French mathematician and legal scholar who lived in the 17th century. He is known for his contributions to number theory, probability, and the theory of optics. He is particularly famous for Fermat’s Last Theorem, which states that there are no non-zero integers a, b, and c that satisfy the equation a^n + b^n = c^n for any value of n greater than 2. This theorem remained unsolved for over 350 years until it was finally proven by Andrew Wiles in 1994.
Fermat was also known for his work in the field of number theory, where he made significant contributions to the study of Diophantine equations and number theory. He also made important contributions to the field of calculus, including the development of the method of tangents, which was an important precursor to the development of calculus by Isaac Newton and Gottfried Leibniz. Despite his many contributions, Fermat was an amateur mathematician who never published his work, and many of his theorems were not discovered until long after his death.
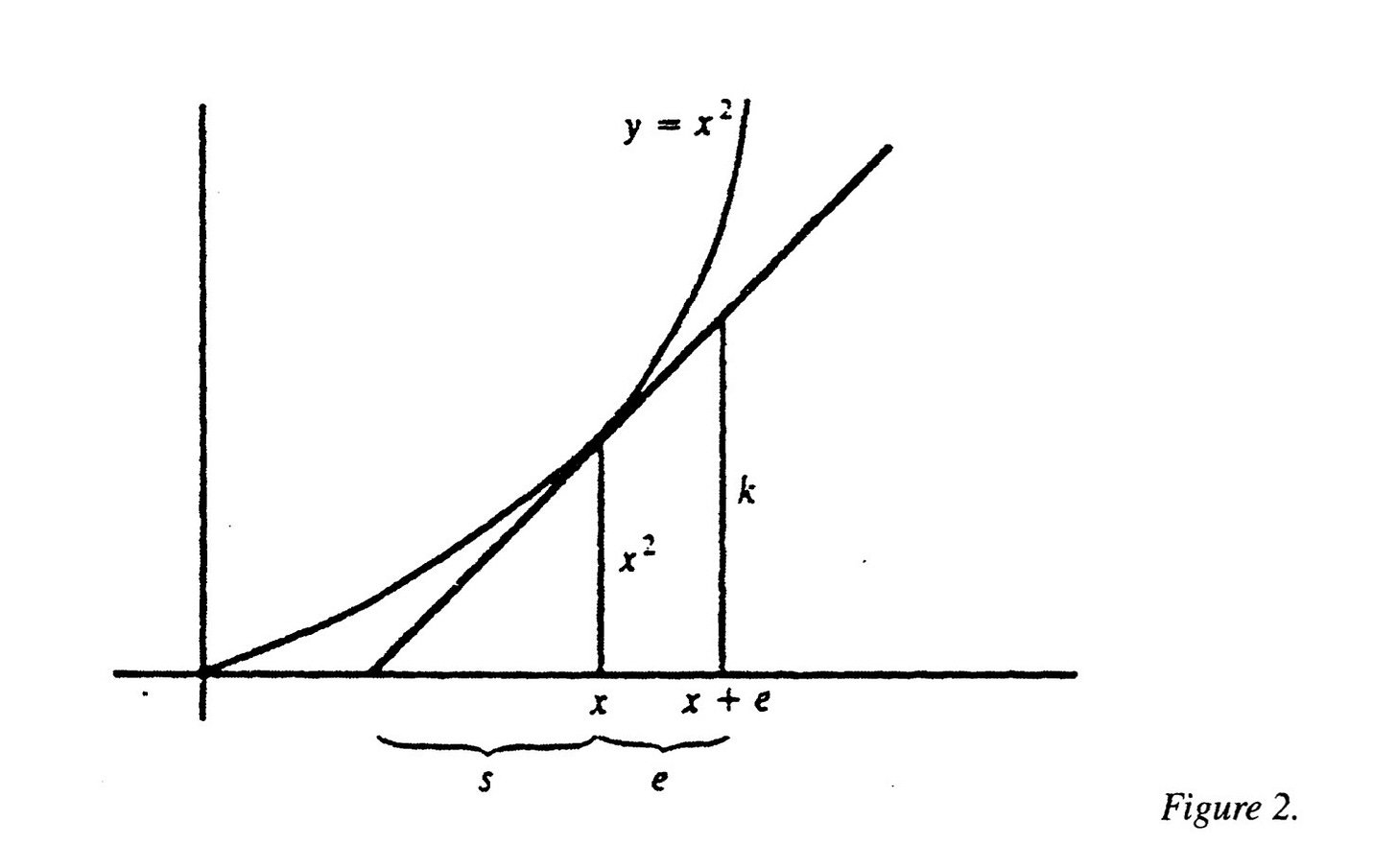
An Illustration: A Parabola
To illustrate, we start by considering a parabola with the equation y = x². We want to find the tangent at some point (x, x²). To do this, we let s denote the subtangent to the curve, which is the tangent lower than the y coordinate of that point.
We now consider the two triangles formed in the figure above. Using the similarity of triangles, we get
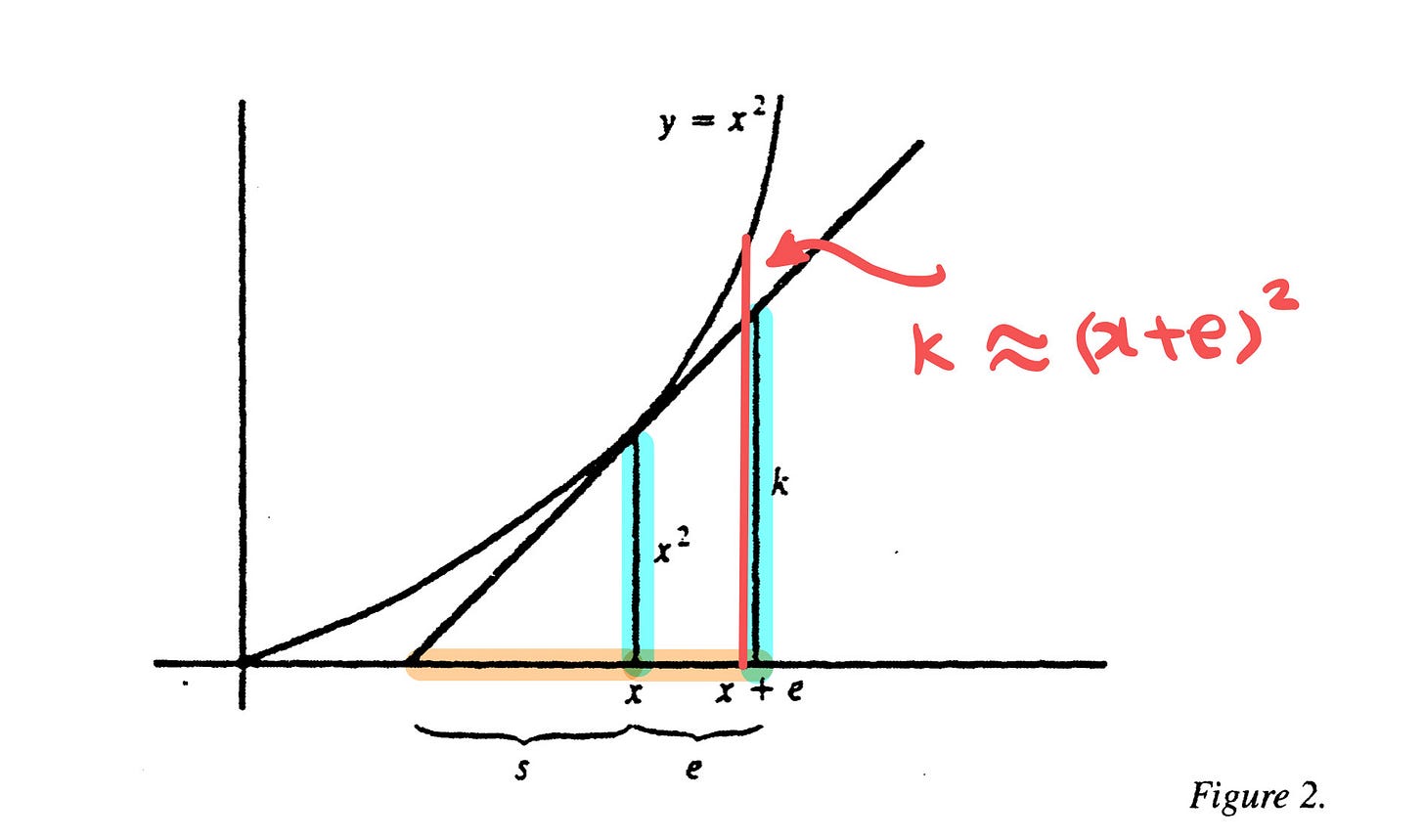
Fermat then reasoned that the length k is ‘adequal’ to (x+e)², meaning k is as close as possible to (x+e)² in length, as denoted in the figure above.
Therefore, we have
Solving for s gives us
Rearranging, we arrive at
Notice x²/s is the rise over run of the first triangle in the figure, Fermat then reasoned that we can simply ‘delete’ the e and the slope to the tangent is 2x.
Under Attack because Something is Wrong
Perhaps, read through the argument above again. Have you noticed any faulty logic with it? In fact, the use of the ‘mysterious e’ gives rise to a contradiction!
Notice in the process of rearranging for s, we divided by e, which means we regard it as not zero. However, in the final argument, Fermat argued that we can ‘delete’ the e to get the gradient of our tangent. That means there’s something wrong with Fermat’s method!
In fact, his attempt at finding the slope of tangents to polynomials gave rise to the concept of the limit, which was introduced formally 200 years later!
And there we have it. We have witnessed some of the endeavours of great minds in the field of mathematics and science!
Happy Reading,
Barry