Garen and Angular Velocity
Physics Challenge From League Of Legends
Today’s Challenge
One of my favourite champions from League of Legends is Garen, the Might of Demacia. They say Garen is a proud and noble warrior, who fights as one of the Dauntless Vanguard.
One of Garen’s abilities is called Judgment, where he rapidly spins his sword around his body, dealing physical damage to nearby enemies.
When he stops spinning his sword, the angular velocity reduces to half after it makes 36 rotations. How many more rotations will the sword make before coming to rest?
The angular deceleration of the sword is uniform.
Give this problem a try before jumping in for the solution!
Solution
I will solve this problem using calculus. Recall the definition of angular velocity
It refers to how fast a rigid body rotates with respect to its centre of rotation. In simple terms, it’s how much the angle has changed at a point during a particular time interval.
If we integrate the angular velocity between two intervals, we will get the net angular displacement between those times.
Therefore, if the total number of rotations is x, we have
where C is a constant depending on our units.
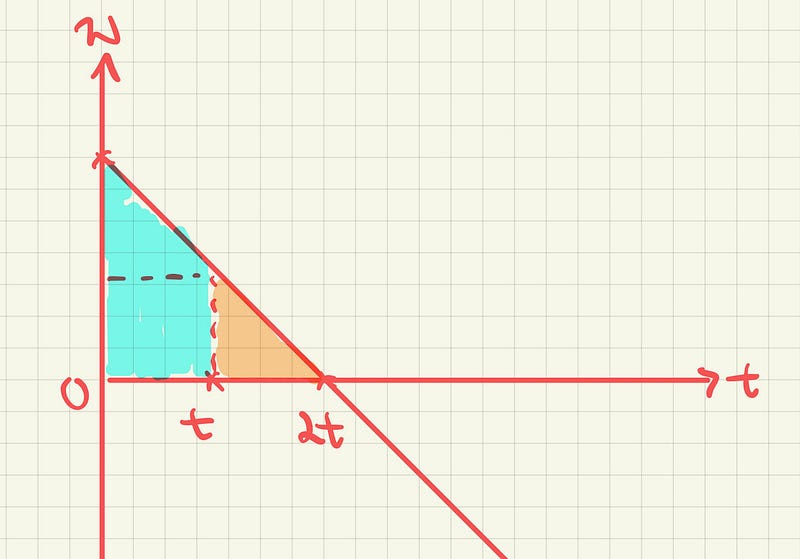
We know that the deceleration of his sword is constant. That means on a graph of omega against t, it’s simply a right triangle as that denotes a constant deceleration.
As the angular deceleration is constant, it takes the same amount of time to slow down from full speed to half speed as it does to slow down from half speed to rest.
The blue and orange areas under the line denote the total number of rotations of the sword between 0 and 2t.
We can use geometry to prove that the blue area is 3 times the green area as follows.
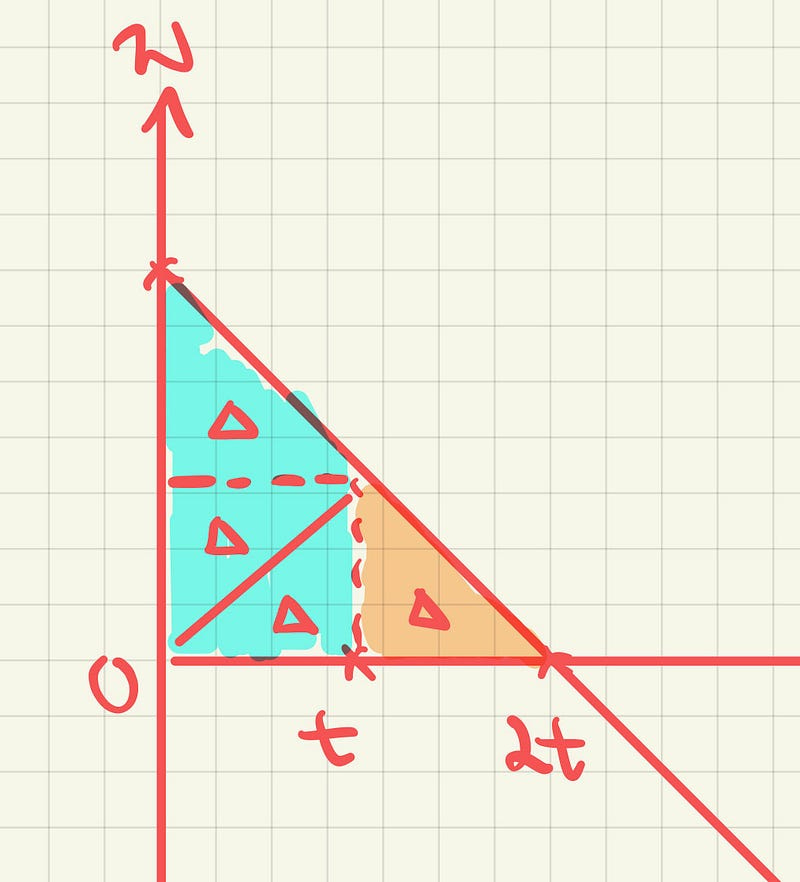
This means the integral of the blue area is 3 times the integral of the orange area, where the blue area is equal to 36 rotations as stated in our problem.
This means
The question states that x1 is 36 as the angular velocity of his sword comes to half after 36 rotations, which means
Garen will spin 12 more times before completely stopping!
Well done! As Garen always says, ‘My heart and sword always for Demacia!’
This is a free newsletter, but if you would like to be one of my early supporters, consider becoming a paid member so that I can continue to bring out quality mathematical treats.
Happy reading,
Barry 🍩