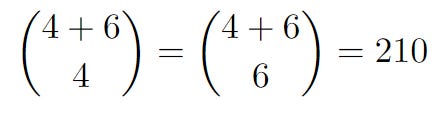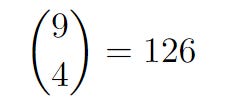Grid Walking Challenge
Combinatorics: Counting
I was on vacation in England, and wanted to visit the Tower of London. The roads were laid out on a grid map, and and the castle was 4 blocks north and 5 blocks east. Unfortunately, there was some police activity near the hotel, and that intersection was blocked off so I could not go through it.
If I were to travel only north and east, how many routes did I have to get to the castle?
Give this problem a try before jumping in for the solution!
Solution
To start with, we will think about the process of me getting to the Tower of London without the police activity in the middle.
Take a look at the grid above, if I start at the bottom left and want to reach the top right corner, I have to move upwards by 4 units and rightwards by 6 units.
For example, I can first go to the right by 2 units, then upwards by 4 units, and finally rightwards by 4 units.
In total, I have to move 10 units in which I can switch the order of those upward or rightward movements.
If we want to find all the possible combinations of routes, that is mathematically equivalent to rearranging the following letters
Mathematically, this is equivalent to the following
In general, for an m × n grid, the number of possible routes is
We will now apply this technique to our problem.
We know that the tower is 4 blocks north and 5 blocks east, so the number of possible routes without any restrictions is
The police are at 2 blocks north and 1 block east. The number of ways to get to the police is
After reaching the police, the number of ways to reach the tower from the police is
So the possible number of routes I have is
We have found the answer!
Bonus Question
Anna and Ben live at opposite corners of a 3 by 4 block.
If Anna only moves right or up or down, and isn’t allowed to retrace her steps, how many ways does she have to get to Ben?
This is a free newsletter, but if you would like to be one of my early supporters, consider becoming a paid member so that I can continue to bring out quality mathematical treats.
☕ Make a one-time coffee donation
Happy reading,
Barry 🍩