MIT Integral Question
Break It Down To Intervals!
We will solve a problem from the 2022 MIT Integration Bee Qualifying Exam.
Give this problem a try before jumping in for the solution!
Solutions
The idea of an integral is to approximate the area of a curvilinear region by breaking the region into infinitesimally thin vertical slabs. With this in mind, let’s look at what happens when we limit the integral to the interval (n, n+1).
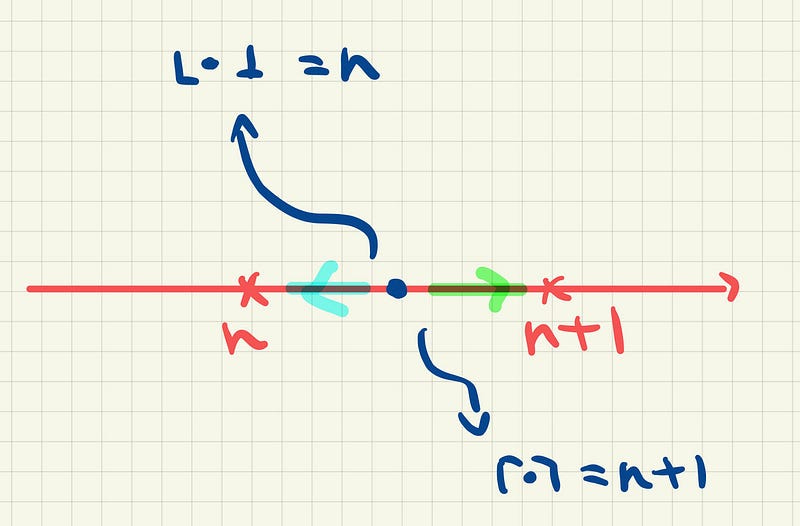
In the interval (n, n+1), we have
As we can see below, the floor and the ceiling functions both take any values between the interval to either the value n or the value n + 1.
The integral we have to evaluate is effectively
Applying the reverse power rule yields us
Upon substituting the values and simplifying, we arrive at
And we have a constant of 1/3!
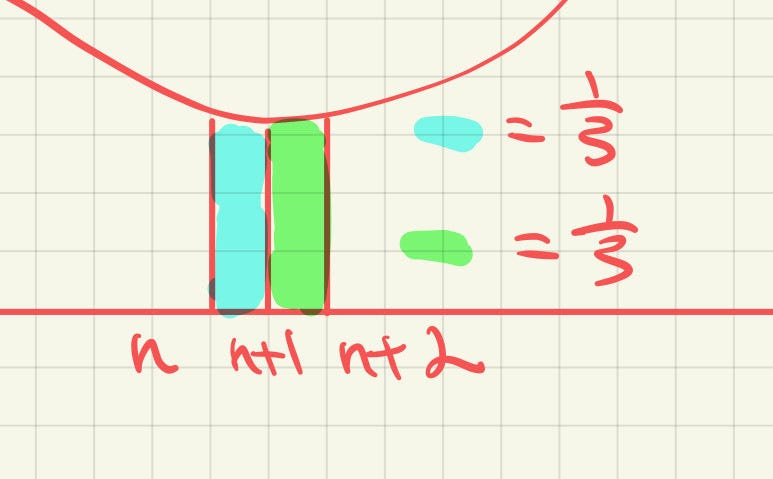
This means that on any arbitrary 1-unit interval (n, n+1), the value of the region under the curve is 1/3.
As the integral aims to evaluate the area from n = 0 to n = 2022, meaning there are 2022 intervals of area 1/3.
The answer is therefore
Well done!
This is a free newsletter, but if you would like to be one of my early supporters, consider becoming a paid member so that I can continue to bring out quality mathematical treats. 🍩
Happy reading,
Barry 🍩