The Elegant Relation Between Pythagoras Theorem and Ptolemy’s Theorem
While geometry is a vast field with lots of abstract and interesting concepts, the Pythagoras Theorem stands out to be the one remembered by most people.
The Pythagoras Theorem states that for a right-angled triangle, the square of the longer side, called the hypotenuse, equals the sum of the squares of the lengths of the shorter sides, called legs. If c is the hypotenuse and a and b are the legs, the theorem is stated as follows: c² = a² + b². The theorem is an important part of geometry and has numerous applications in maths and physics.
However, the Pythagoras Theorem turns out to be a special case of another lesser-known theorem, the Ptolemy’s Theorem. To understand why, let’s take a look at the Ptolemy’s Theorem.
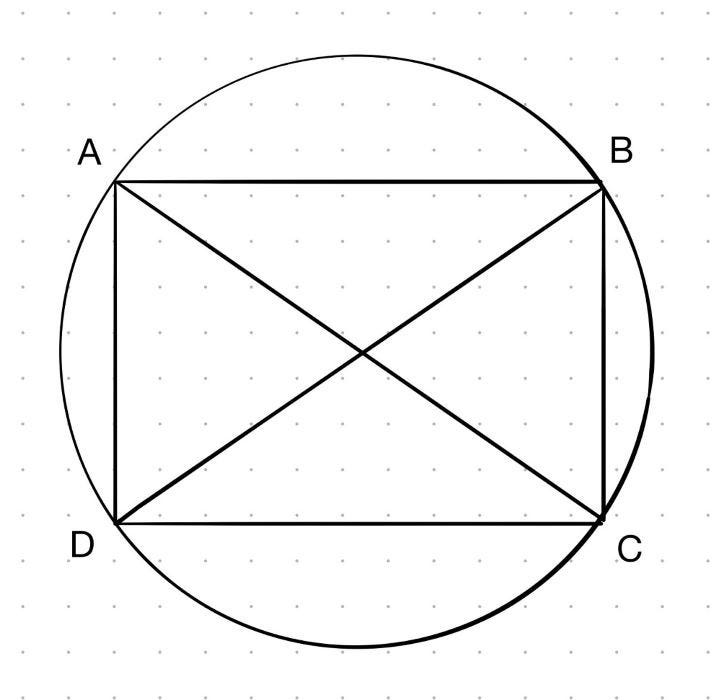
The Ptolemy’s Theorem states the relationship between the four sides and the two diagonals of a cyclic quadrilateral. It states that if a quadrilateral is inscribed in a circle, then the product of the lengths of the diagonals equals the sum of the products of the lengths of the pairs of opposite sides: AC ×BD = AB × CD + AD × BC.
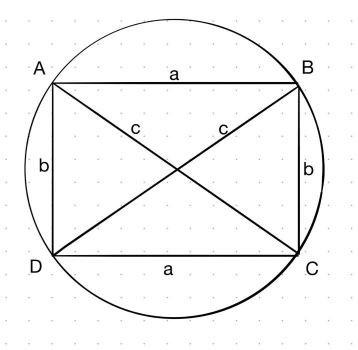
And since a rectangle is also a quadrilateral, let’s see what happens when the cyclic quadrilateral becomes a rectangle.
Using the Ptolemy’s Theorem, we get AC ×BD = AB × CD + AD × BC. Since this is a rectangle, the opposite sides are of the same length and so are the diagonals. And if the diagonals are c and the sides are a and b respectively, we get c² = a² + b², which is precisely the Pythagoras Theorem!
In short, the Pythagoras Theorem is simply the special case of the Ptolemy’s Theorem when the inscribed quadrilateral is a rectangle.
This is a free newsletter, but if you would like to be one of my early supporters, consider becoming a paid member so that I can continue to bring out quality mathematical treats. 🍩
Happy reading,
Barry 🍩