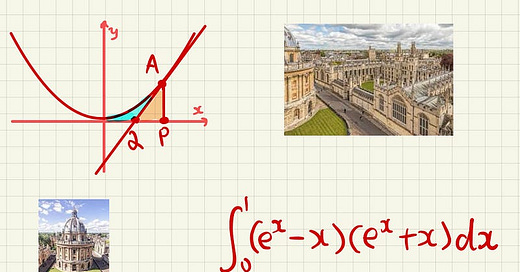Two Oxford Admission Questions
Differentiation and Integration
In today’s entry, we will look at two Oxford admission questions on the Oxford MAT 2020.
Join our vibrant community and become a paid member today!
Question 1
Solution 1:
To solve the first integral, we will use the formula for the difference of two squares. Our integral becomes
Using reverse chain and reverse product rule, our integral is
substituting the limits gives us
The answer is D.
Question 2
To solve this question, we will first have to find the equation of the tangent line.
Using differential calculus, we find the derivative of the curve
We are given an arbitrary point (a, a²). As we have a point and the slope, we can find the equation of the tangent at point x = a.
This simplifies to
Now that we have the original parabola and the equation of tangent, let’s put this information onto a coordinate plane.
The coordinates of Q are at the x-intercept of our tangent, which can be found by substituting y = 0.
We are asked to find the area of the region bounded by the parabola, the tangent line and the x-axis. This is the area shaded in blue.
The area shaded in blue can be found by
Mathematically, that is
Upon integrating and simplifying, we arrive at our answer
Well done!
This is a free newsletter, but if you would like to be one of my early supporters, consider becoming a paid member so that I can continue to bring out quality mathematical treats.
Happy reading,
Barry 🍩