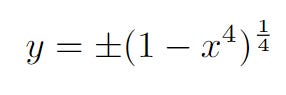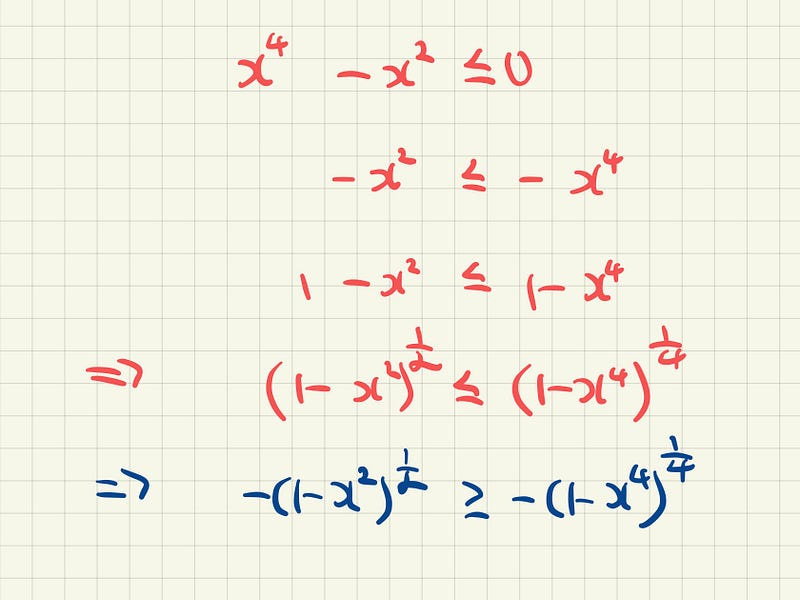Today’s Deep Dive
What does x¹⁰⁰ + y¹⁰⁰ = 1 look like? What about x²⁰²³ + y²⁰²³ = 1? What about its general form? To answer these questions, we will start from the fundamentals and work our way up!
(This is a very rewarding post for those who have the courage to stick to it!)
Feel free to pause at each section and think through this very mesmerising exploration!
The Unit Circle 🐺
Our journey starts at high school level algebra. In fact, we will revise the concept of the unit circle.
Below is the equation of the unit circle
It is centred at the origin on the Cartesian plane with radius 1.
For a more general equation, we have
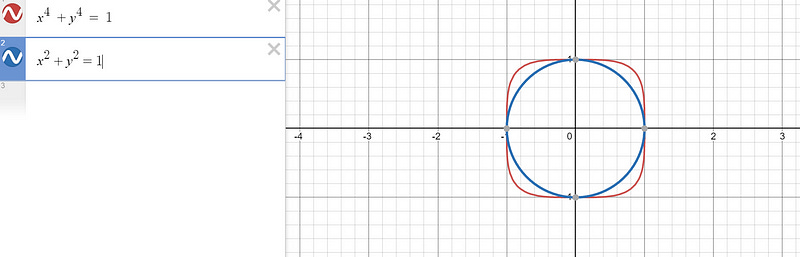
What about x⁴ + y⁴ = 1? 🦋
Now that we have a basic understanding of the equation of the unit circle, can we use sketch the curve x⁴ + y⁴ = 1 using this information? And what happens as the powers become bigger even integers?
An important skill for sketching unfamiliar functions is to consider the intercepts on both axes.
Substituting x = 0 gives us y-intercepts at x = 1 and x = -1. Likewise, putting y = 0 gives us x-intercepts at y = 1 and y = -1.
Looking at our unit circle, we know that our new curve intersects with the unit circle at both axes.
We can unearth another piece of important information about our equation by rearranging it into the form with y as the subject.
In this case, we have
and the unit circle has the equation
For -1 ≤ x ≤ 1, we have the initial inequality
And proceed as follows
What can we say about these two inequalities? In fact, this shows us that the unit circle is bounded by the equation x⁴ + y⁴ = 1!
Try playing around with different even integer powers and observe the behaviour of the graphs.
What happens when the powers are 100 or even 1000? It looks like the curve is becoming a square as the powers increase to higher even integers.
Interestingly, if you actually zoom in on the graphs and look at the corners, you will notice that it’s in fact a rounded shape and the corners are smooth. And that is true no matter how big the powers are, the graph will never become a square.
But why is that?
Unfolding the Mystery 🐰
In general, the above equation for integers k is differentiable at every single point. In real analysis, our equation is said to be smooth.
We know that a square has four sharp corners, similar to the absolute value function f(x) = |x|, it is not differentiable at point x = 0.
Intuitively, we cannot draw a tangent at a corner as we do at an arbitrary point on a curve. Because non-differentiable curves can only be generated using special mathematical operators like the modulus sign, our equation that consists of polynomials alone does not have sharp corners and therefore cannot be a square.
Wait, there’s more 🐇🐇
What about x³ + y³ = 1? 🦁
The equations discussed thus far all consist of even integer powers.
x³ + y³ = 1 is a function because, for every y value, there is only one corresponding x value.
x² + y² = 1 is not a function for every y value, there is more than one corresponding x value.
We can rearrange the function as follows
We find that the curve crosses points (0,1) and (1,0) by evaluating the intercepts on both axes.
If we consider the interval 0≤ x ≤ 1, the function gives us a similar shape of a circle in the first quadrant.
To sketch other parts of the curve, let’s consider what happens when x approaches ±infinity. We can intuitively see that as x becomes a bigger and bigger value, the effect of 1 becomes negligible and our equation is approximately
Surprisingly, we have delved into the idea of oblique asymptotes! The function will approach the line y = -x for both positive and negative x values!
looks like a boa constrictor?? Little Prince??
Asymptotes in a Nutshell 🤴
The idea of asymptotes is introduced when we look at reciprocal functions like f(x) = 1/x. The domain is all real numbers except for 0. Division by 0 is a common theme in functions involving asymptotes.
An oblique asymptote can instead be found by evaluating the function at extreme values of x!
Oblique asymptotes are like your really good friends; you can cross them, but you’ll stay close in the end.
This is a free newsletter, but if you would like to be one of my early supporters, consider becoming a paid member so that I can continue to bring out quality mathematical treats.
☕ Make a one-time coffee donation
Happy reading,
Barry 🍩