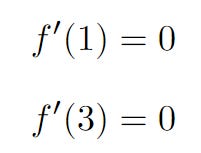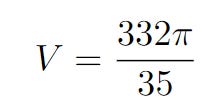What’s The Volume Of The Vase?
A Very Very Interesting Calculus Problem
A vase maker decides to construct a vase whose contour is a cubic polynomial according to the following specifications:
The vase is 4 feet tall.
The vase is 4 feet in diameter at its widest (which occurs at 1 foot from the base)
The vase is 2 feet in diameter at its narrowest (which occurs at 1 foot from the top)
The vase has a flat circular bottom
What is the volume of the vase in cubic feet?
Give this problem a try before jumping in for the solution!
Solution
The thought process behind coming up with a solution should be to figure out the cubic polynomial using the given information.
In general, a cubic polynomial can be written as
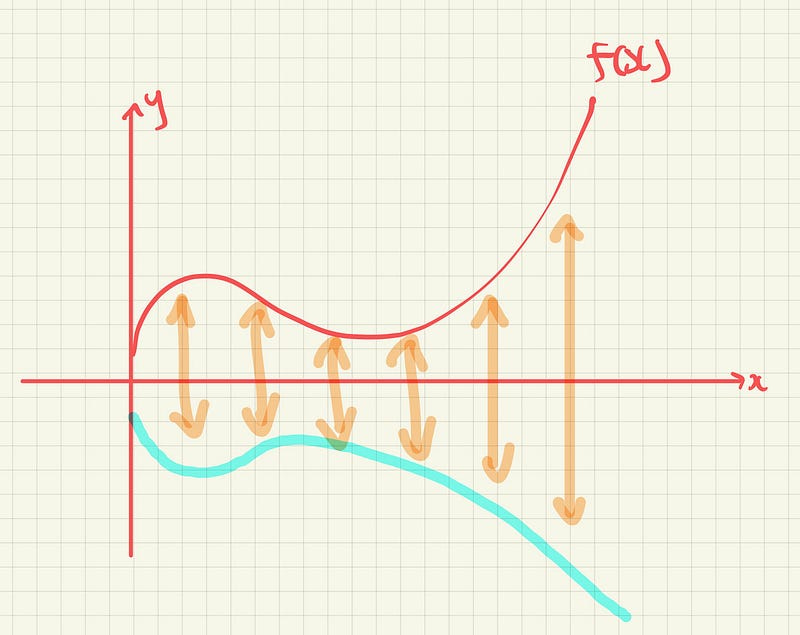
The contour of the vase when plotted on the Cartesian plane should look something like this
We are interested in finding the volume of revolution of the object made from rotating the function along the x-axis.
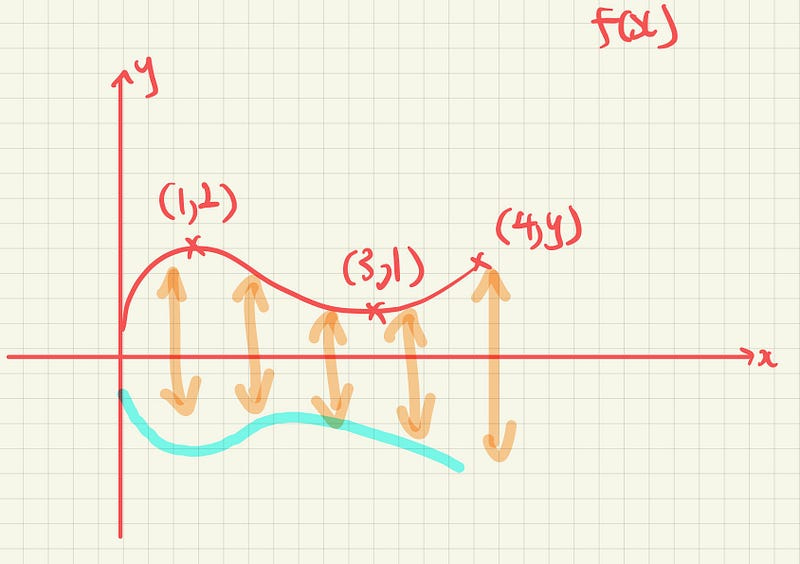
As the vase is 4 feet wide in diameter at its widest at 1 foot from the bottom, we can translate this onto the graph by saying that f(x) passes through (1,2).
The x-coordinate is the height from the base. The y-coordinate is half of 4 because as the object rotates around the x-axis, its value doubles.
Similarly, as the vase is 2 feet wide in diameter at its narrowest at 1 foot from the top, we can translate this onto the graph by saying that f(x) passes through (3,1).
The x-coordinate is 3 because the vase is 4 feet tall and 4 -1 = 3. The y-coordinate is 1 for the same reason stated above.
Graphically, that is
Notice (1,2) and (3,1) are local extrema, which means
for which f’(x) =
Now that we have 4 equations in 4 unknowns, let's write them out explicitly
On solving, we should get
Therefore, our function is
Let’s see what the function looks like
As the vase is 4 feet tall, we will integrate the above function from 0 to 4 as follows
As we can see, this will be a very long polynomial. So with the help of technology, we can find that
Well done!
🧩 My name is Barry and I study mathematics at the University of Warwick. I write this newsletter in my free time to share the joy and art of mathematics through problems and puzzles. 🧩
If you would like to be one of my early supporters, consider becoming a paid member so that I can continue to bring out quality mathematical treats. 🍭
Happy reading,
Barry 🍩