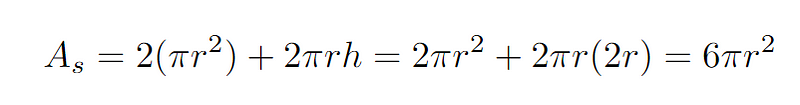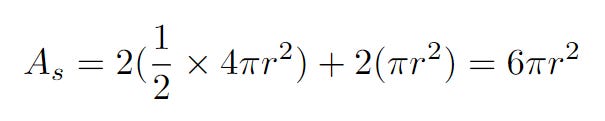Which Shape Has A Larger Surface Area?
Think Carefully!
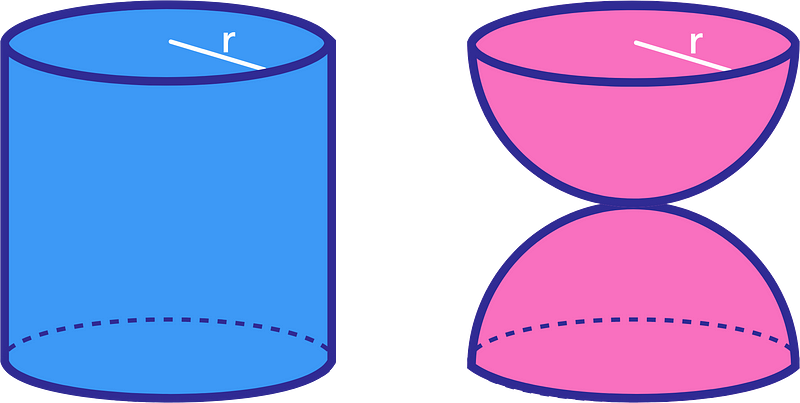
The red figure at the right is made of two hemispheres of equal radius. The blue cylinder at the left has the same radius and height as the red figure.
Which shape has a larger surface area?
Give this problem a try before jumping in for the solution!
Solution
We will find an expression for both the cylinder and the two hemispheres with algebra.
We let h denote the height of the blue cylinder. Notice that the blue cylinder has a height equivalent to the height of the two hemispheres.
We know that the total surface area of a cylinder is equal to the sum of areas of the two base circles and the curved rectangular side.
Mathematically, it is
The total surface area of the two hemispheres in pink is equal to the sum of the curved surface area and the sum of the two base circles (one on top, one at the bottom). And the curved surface area of each of these hemispheres is half the surface area of a sphere.
Mathematically, it is
Therefore, they have the same surface area!
Some observation
The two figures are composed of two base circles and their curved surface area respectively. Interestingly, the curve surface area of the sphere is equal to the curved surface area of the cylinder. This might seem counterintuitive because the sphere has gotten smaller in volume!
This is a free newsletter, but if you would like to be one of my early supporters, consider becoming a paid member so that I can continue to bring out quality mathematical treats. 🍩
Happy reading,
Barry 🍩