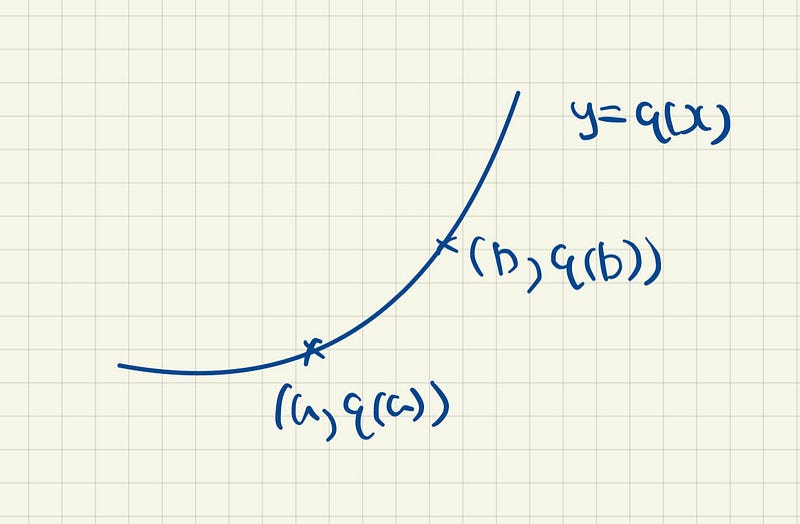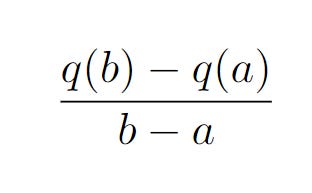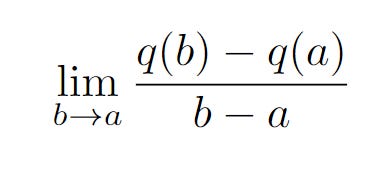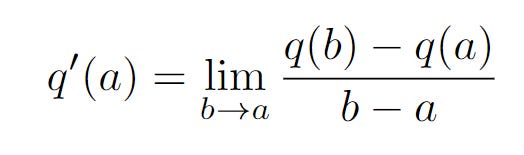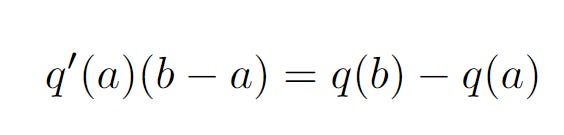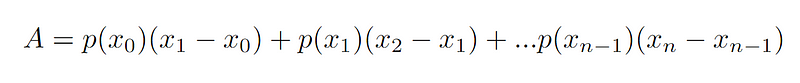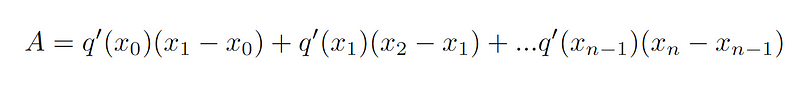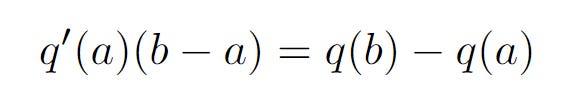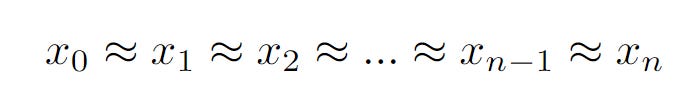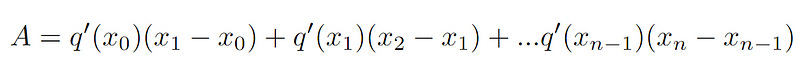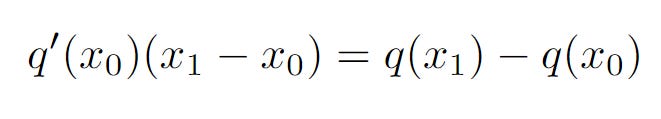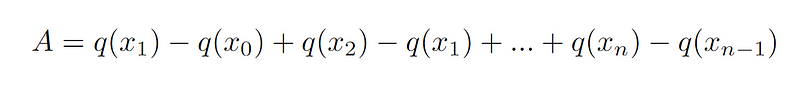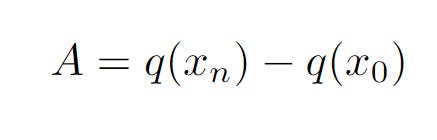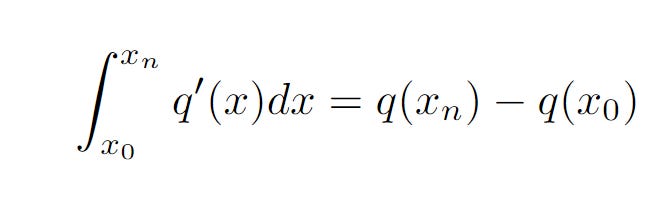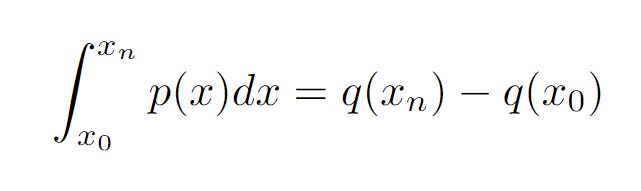Why Does The Definite Integral Equal Area?
The Fundamental Theorem Of Calculus
If you have taken high school calculus, you probably have computed a definite integral to find the area under a curve. But have you ever thought about the relation between the two, in particular, why the value of the definite integral gives us the area under the curve. Well, I am glad you have stumbled upon this article because I am about to guide you through the thought process behind it.
Without further ado, let’s dive in!
To start with, recall the idea of the derivative. In a nutshell, it’s bringing two points on a curve closer and closer together and finding the gradient at that particular point.
Now consider a function y = q(x). We then pick two arbitrary points on the curve, (a, q(a)) and (b, q(b)).
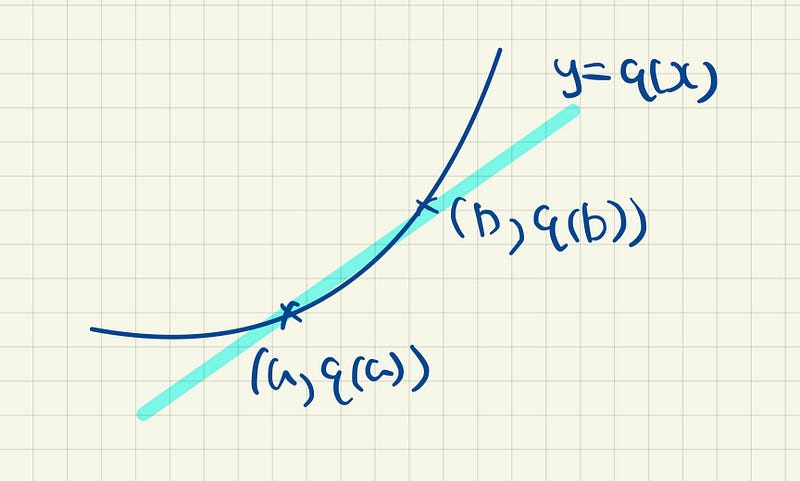
If we want to find the gradient of these two points, we have
But this expression gives us the slope of two points, a and b. We are interested in finding the gradient at one point, which is a. We will have the following limit.
This is equivalent to the idea behind the derivative, bringing point b closer and closer to a. Which means, this is the derivative of the function q(x) at a.
Therefore, we have
However, when b is really close to a, we can get rid of our limit notation and say
Let’s keep this formula in mind for now.
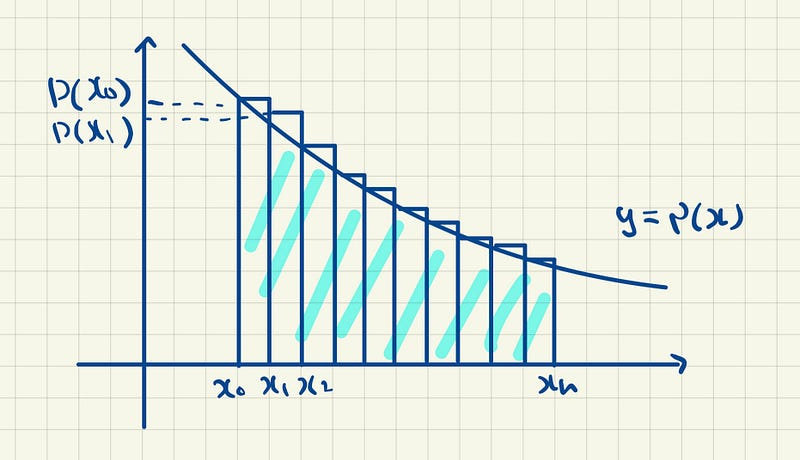
We will now consider the area under a particular function, y = p(x).
We have n thin strips of rectangles from x0 to xn. The area of the sum of n strips of rectangles is
If we now let q’(x) = p(x), we have
What we have done is essentially rewrite the formula in terms of q’(x).
Now have you noticed similar? Notice each expression is equivalent to the formula we have derived above.
This formula has one condition: when a is very very close to b.
Now, going back to our area of thin strips of rectangles, the value of the area is equal to the area under the curve when there are an infinite number of thin strips, meaning n tends to infinity. This also means the x0, x1, x2 … are very close to each other.
This means we can apply the formula above to our expression of thin strips of triangles.
We will have
Therefore, our expression becomes
The terms cancel out and we will now be left with
Does that look familiar to you? Well, it should and you are about to find out why.
What we have done is compute the area under the function y = p(x) from x0 to xn.
So using notation from integral calculus, we have
But we have also defined p(x) = q’(x), so we have
The right-hand side of our equation is the area of the curve and the left-hand side is the notation of our integral. We have completed our proof!
This is a free newsletter, but if you would like to be one of my early supporters, consider becoming a paid member so that I can continue to bring out quality mathematical treats. 🍩
Happy reading,
Barry 🍩